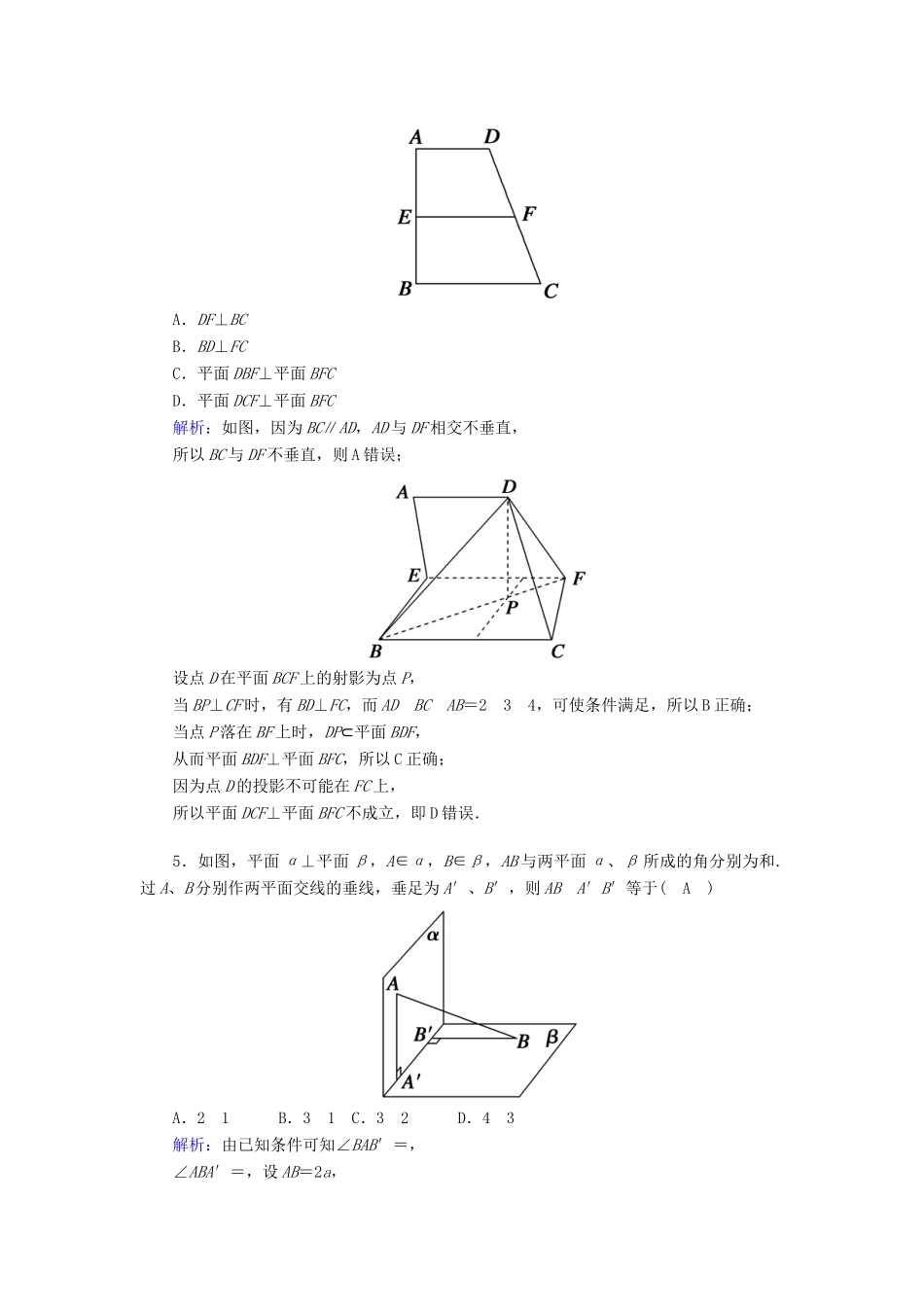
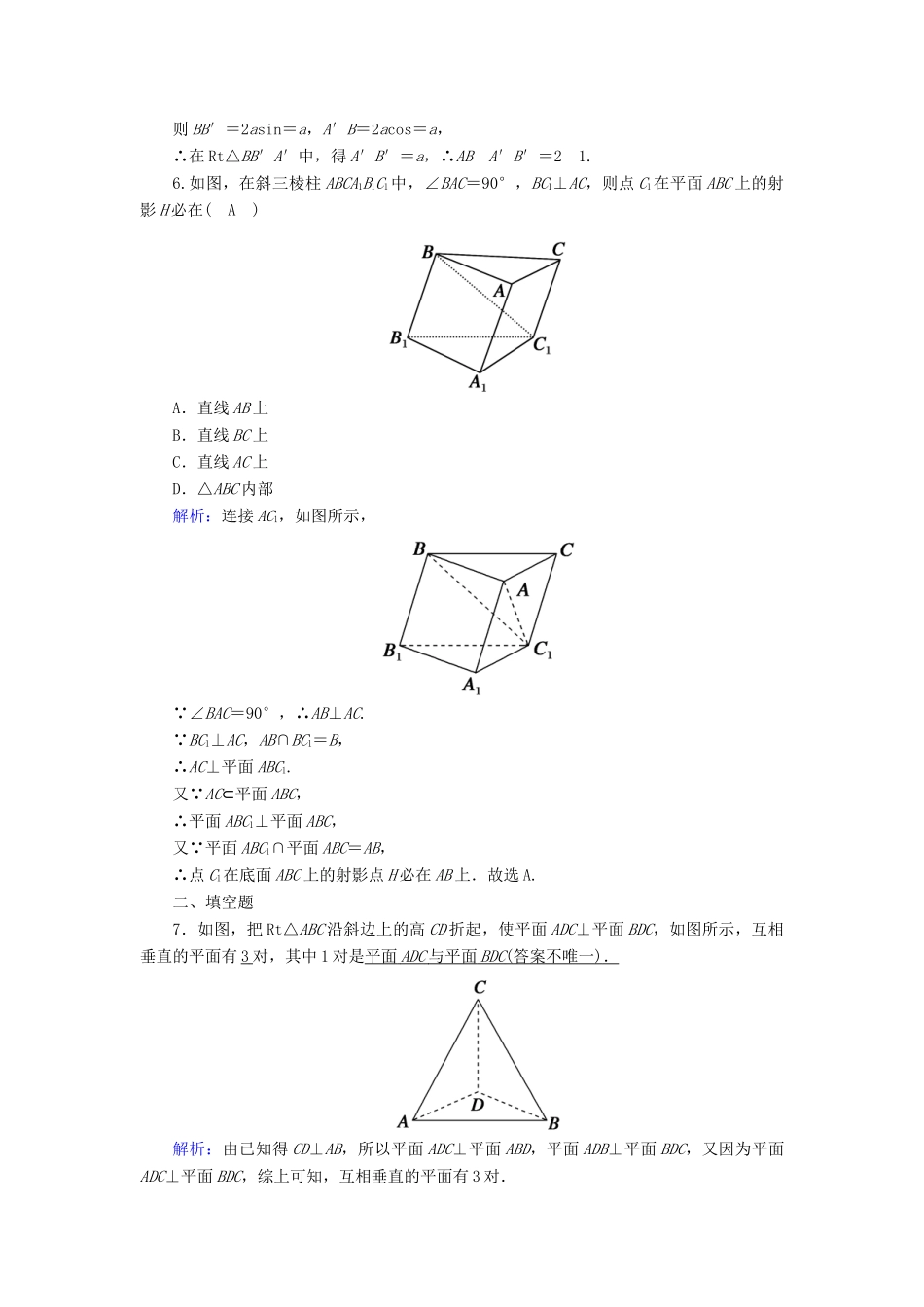
课时作业37平面与平面垂直的性质时间:45分钟——基础巩固类——一、选择题1.已知直线m,n和平面α,β,若α⊥β,α∩β=m,n⊂α,要使n⊥β,则应增加的条件是(B)A.m∥nB.n⊥mC.n∥αD.n⊥α解析:由面面垂直的性质定理知,要使n⊥β,应有n与交线m垂直,∴应增加条件n⊥m.2.下列命题中错误的是(D)A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γD.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β解析:由平面与平面垂直的有关性质可以判断出D项错误.3.如图所示,三棱锥PABC中,平面ABC⊥平面PAB,PA=PB,AD=DB,则(B)A.PD⊂平面ABCB.PD⊥平面ABCC.PD与平面ABC相交但不垂直D.PD∥平面ABC解析: PA=PB,AD=DB,∴PD⊥AB.又 平面ABC⊥平面PAB,平面ABC∩平面PAB=AB,∴PD⊥平面ABC.4.(多选)如图,在梯形ABCD中,AD∥BC,∠ABC=90°,ADBCAB=234,E,F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折,给出四个结论,在翻折过程中,可能成立的结论的为(BC)A.DF⊥BCB.BD⊥FCC.平面DBF⊥平面BFCD.平面DCF⊥平面BFC解析:如图,因为BC∥AD,AD与DF相交不垂直,所以BC与DF不垂直,则A错误;设点D在平面BCF上的射影为点P,当BP⊥CF时,有BD⊥FC,而ADBCAB=234,可使条件满足,所以B正确;当点P落在BF上时,DP⊂平面BDF,从而平面BDF⊥平面BFC,所以C正确;因为点D的投影不可能在FC上,所以平面DCF⊥平面BFC不成立,即D错误.5.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为和.过A、B分别作两平面交线的垂线,垂足为A′、B′,则ABA′B′等于(A)A.21B.31C.32D.43解析:由已知条件可知∠BAB′=,∠ABA′=,设AB=2a,则BB′=2asin=a,A′B=2acos=a,∴在Rt△BB′A′中,得A′B′=a,∴ABA′B′=21.6.如图,在斜三棱柱ABCA1B1C1中,∠BAC=90°,BC1⊥AC,则点C1在平面ABC上的射影H必在(A)A.直线AB上B.直线BC上C.直线AC上D.△ABC内部解析:连接AC1,如图所示, ∠BAC=90°,∴AB⊥AC. BC1⊥AC,AB∩BC1=B,∴AC⊥平面ABC1.又 AC⊂平面ABC,∴平面ABC1⊥平面ABC,又 平面ABC1∩平面ABC=AB,∴点C1在底面ABC上的射影点H必在AB上.故选A.二、填空题7.如图,把Rt△ABC沿斜边上的高CD折起,使平面ADC⊥平面BDC,如图所示,互相垂直的平面有3对,其中1对是平面ADC与平面BDC(答案不唯一).解析:由已知得CD⊥AB,所以平面ADC⊥平面ABD,平面ADB⊥平面BDC,又因为平面ADC⊥平面BDC,综上可知,互相垂直的平面有3对.8.已知直二面角αlβ,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则CD的长为.解析:如图,连接BC, 二面角αlβ为直二面角,AC⊂α,且AC⊥l,∴AC⊥β,又BC⊂β,∴AC⊥BC,∴BC2=AB2-AC2=3,又BD⊥CD,∴CD==.9.如图,若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直,则cosαcosβ=2.解析:由题意,两个矩形的对角线长分别为5,2,所以cosα==,cosβ=,所以cosαcosβ=2.三、解答题10.把一副三角板如图拼接,设BC=6,∠BAC=90°,AB=AC,∠BCD=90°,∠D=60°,使两块三角板所在的平面互相垂直.求证:平面ABD⊥平面ACD.证明: 平面ABC⊥平面BCD,CD⊥BC,∴CD⊥平面ABC.又AB⊂平面ABC,∴CD⊥AB,又AB⊥AC,CD∩AC=C,∴AB⊥平面ACD.又AB⊂平面ABD,∴平面ABD⊥平面ACD.11.如图,在三棱锥PABC中,E,F分别为AC,BC的中点.(1)求证:EF∥平面PAB;(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°.求证:平面PEF⊥平面PBC.证明:(1) E,F分别为AC,BC的中点,∴EF∥AB.又EF⊄平面PAB,AB⊂平面PAB,∴EF∥平面PAB.(2) PA=PC,E为AC的中点,∴PE⊥AC.又 平面PAC⊥平面ABC,∴PE⊥平面ABC,∴PE⊥BC.又 F为BC的中点,∴EF∥AB. ∠ABC=90°,∴BC⊥EF. EF∩PE=E,∴BC⊥平面PEF.又 BC⊂平面PBC,∴平面PBC⊥平面PEF.——能...