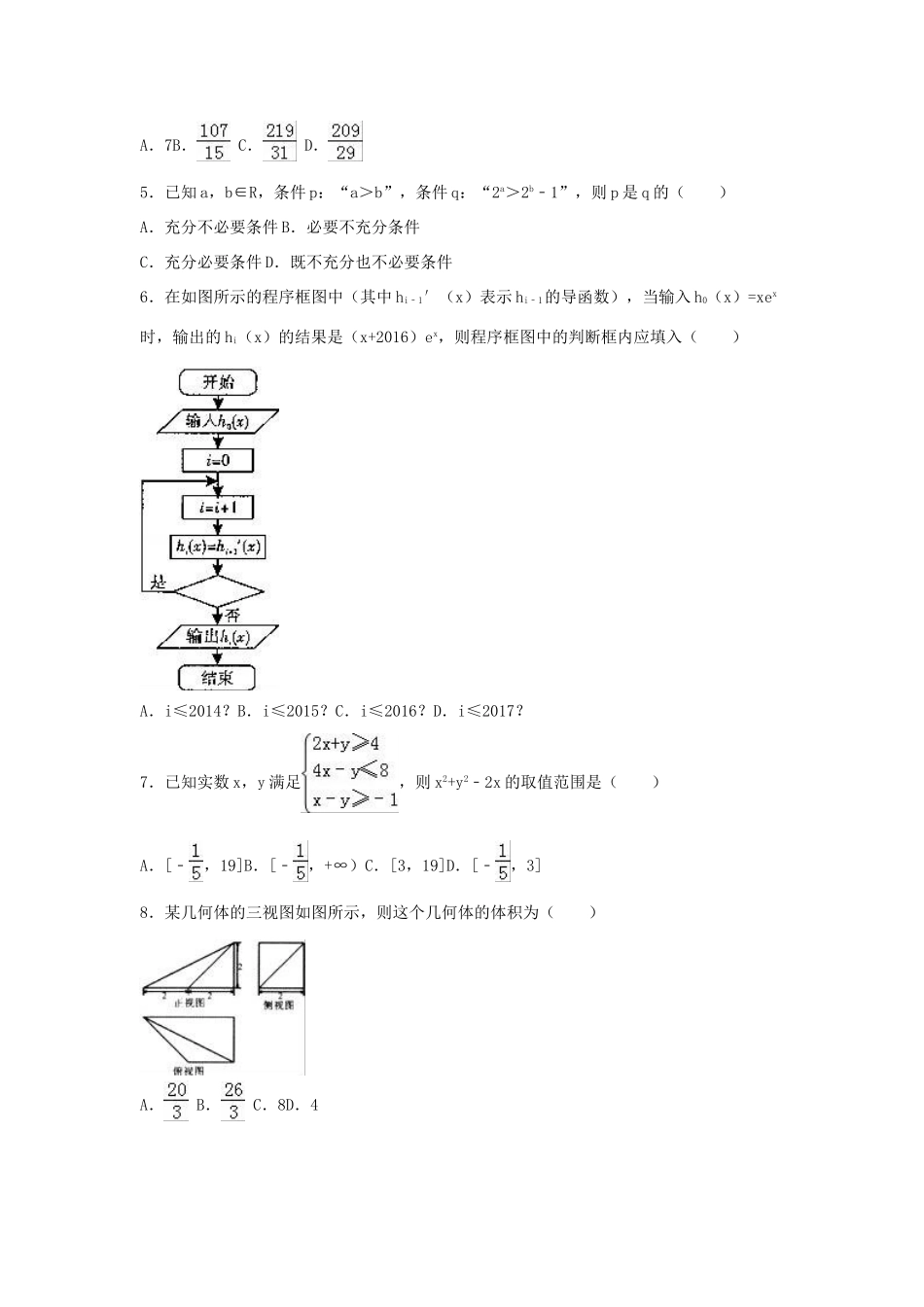
2016年河北省衡水市武邑中学高考数学冲刺试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U=R,则正确表示集合M={﹣1,0,1}和N={x|x2+x=0}关系的韦恩(Venn)图是()A.B.C.D.2.若z=(a﹣)+ai为纯虚数,其中a∈R,则=()A.iB.1C.﹣iD.﹣13.从一批待测物品中随机抽测100件的重量(单位:kg),将所得数据绘制成如图所示的频率分布直方图,估计这批物品的平均重量(单位:kg)为()A.11B.11.5C.12D.12.54.《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:第2天开始,每天比前天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织390尺布”,则该女第5天所织的布的尺数为()A.7B.C.D.5.已知a,b∈R,条件p:“a>b”,条件q:“2a>2b﹣1”,则p是q的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.在如图所示的程序框图中(其中hi﹣1′(x)表示hi﹣1的导函数),当输入h0(x)=xex时,输出的hi(x)的结果是(x+2016)ex,则程序框图中的判断框内应填入()A.i≤2014?B.i≤2015?C.i≤2016?D.i≤2017?7.已知实数x,y满足,则x2+y2﹣2x的取值范围是()A.[﹣,19]B.[﹣,+∞)C.[3,19]D.[﹣,3]8.某几何体的三视图如图所示,则这个几何体的体积为()A.B.C.8D.49.已知f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)满足f(x)=﹣f(x+),对任意x都有f(x)≤f()=3,则g(x)=2cos(ωx+φ)在区间[0,]上的最大值为()A.4B.C.1D.﹣210.已知菱形ABCD的边长为2,∠BAD=120°,点E、F分别在边BC、DC上,=λ,=μ,若•=1,•=﹣,则λ+μ=()A.B.C.D.11.已知双曲线M的焦点F1,F2在x轴上,直线是双曲线M的一条渐近线,点P在双曲线M上,且,如果抛物线y2=16x的准线经过双曲线M的一个焦点,那么=()A.21B.14C.7D.012.设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为()A.[1,+∞)B.(﹣∞,1]C.(﹣∞,2]D.[2,+∞)二、填空题(本大题共4小题,每小题5分,共20分)13.的展开式中常数项为.14.△ABC中,内角A、B、C对的边分别为a、b、c,如果△ABC的面积等于8,a=5,tanB=﹣,那么=.15.将一颗质地均匀的骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设任意投掷两次使直线l1:x+ay=3,l2:bx+6y=3平行的概率为P1,不平行的概率为P2,若点(P1,P2)在圆(x﹣m)2+y2=的内部,则实数m的取值范围是.16.若函数f(x)=(4﹣x2)(ax2+bx+5)的图象关于直线对称,则f(x)的最大值是.三、解答题(解答应写出文字说明、证明过程或演算步骤)17.已知数列{an}中,a1=,an+1=(n∈N*)(1)求证:数列{﹣1}是等比数列,并求{an}的通项公式an;(2)设bn=,求证:<2.18.现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(Ⅰ)求该射手恰好命中一次得的概率;(Ⅱ)求该射手的总得分X的分布列及数学期望EX.19.如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.(Ⅰ)求证:平面EAC⊥平面PBC;(Ⅱ)若二面角P﹣AC﹣E的余弦值为,求直线PA与平面EAC所成角的正弦值.20.已知椭圆C:=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=.(I)求椭圆C的方程;(Ⅱ)与抛物线相切于第一象限的直线l,与椭圆交于A,B两点,与x轴交于M点,线段AB的垂直平分线与y轴交于N点,求直线MN斜率的最小值.21.已知函数f(x)=(Ⅰ)若m∈(﹣2,2),求函数y=f(x)的单调区间;(Ⅱ)若m∈(0,],则当x∈[0,m+1)时,函数y=f(x)的图象是否总...