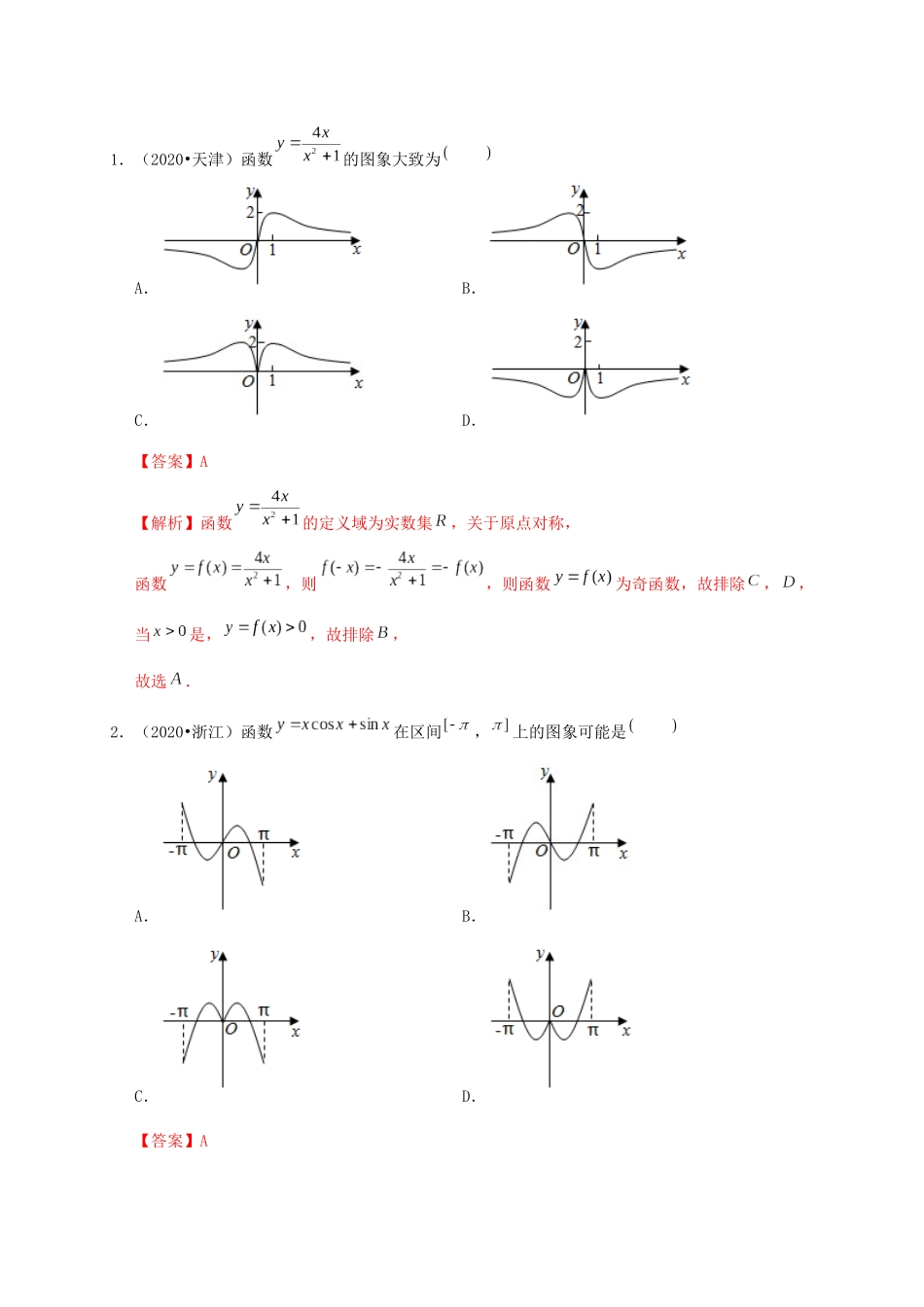
函数的图象1.描点法作图方法步骤:(1)确定函数的定义域.(2)化简函数的解析式.(3)讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋势).(4)描点连线,画出函数的图象.2.图象变换(1)平移变换(2)对称变换①y=f(x)―――――→y=-f(x).②y=f(x)―――――→y=f(-x).③y=f(x)―――――→y=-f(-x).④y=ax(a>0且a≠1)―――――→y=logax(a>0且a≠1).(3)伸缩变换①y=f(x)―――――――――――――――――――→――――――――――――――――――――→y=f(x).②y=f(x)―――――――――――――――――――→y=af(x).(4)翻折变换①y=f(x)――――――――――→y=|f(x)|.②y=f(x)―――――――――――→y=f(|x|).概念方法微思考1.函数f(x)的图象关于直线x=a对称,你能得到f(x)解析式满足什么条件?提示f(a+x)=f(a-x)或f(x)=f(2a-x).2.若函数y=f(x)和y=g(x)的图象关于点(a,b)对称,则f(x),g(x)的关系是g(x)=2b-f(2a-x).1.(2020•天津)函数的图象大致为A.B.C.D.【答案】A【解析】函数的定义域为实数集,关于原点对称,函数,则,则函数为奇函数,故排除,,当是,,故排除,故选.2.(2020•浙江)函数在区间,上的图象可能是A.B.C.D.【答案】A【解析】,则,为奇函数,函数图象关于原点对称,故排除,,当时,,故排除,故选.3.(2019•新课标Ⅲ)函数在,的图象大致为A.B.C.D.【答案】B【解析】由在,,知,是,上的奇函数,因此排除又(4),因此排除,.故选.4.(2019•浙江)在同一直角坐标系中,函数,且的图象可能是A.B.C.D.【答案】D【解析】由函数,,当时,可得是递减函数,图象恒过点,函数,是递增函数,图象恒过,;当时,可得是递增函数,图象恒过点,函数,是递减函数,图象恒过,;满足要求的图象为:故选.5.(2019•新课标Ⅰ)函数在,的图象大致为A.B.C.D.【答案】D【解析】,,,,为,上的奇函数,因此排除;又,因此排除,;故选.6.(2018•新课标Ⅱ)函数的图象大致为A.B.C.D.【答案】B【解析】函数,则函数为奇函数,图象关于原点对称,排除,当时,(1),排除.当时,,排除,故选.7.(2018•新课标Ⅲ)下列函数中,其图象与函数的图象关于直线对称的是A.B.C.D.【答案】B【解析】首先根据函数的图象,则:函数的图象与的图象关于轴对称.由于函数的图象关于直线对称.则:把函数的图象向右平移2个单位即可得到:.即所求得解析式为:.故选.8.(2018•浙江)函数的图象可能是A.B.C.D.【答案】D【解析】根据函数的解析式,得到:函数的图象为奇函数,故排除和.当时,函数的值也为0,故排除.故选.9.(2018•上海)设是含数1的有限实数集,是定义在上的函数,若的图象绕原点逆时针旋转后与原图象重合,则在以下各项中,(1)的可能取值只能是A.B.C.D.0【答案】B【解析】由题意得到:问题相当于圆上由12个点为一组,每次绕原点逆时针旋转个单位后与下一个点会重合.我们可以通过代入和赋值的方法当(1),,0时,此时得到的圆心角为,,0,然而此时或者时,都有2个与之对应,而我们知道函数的定义就是要求一个只能对应一个,因此只有当,此时旋转,此时满足一个只会对应一个,因此答案就选:.故选.10.(2018•新课标Ⅲ)函数的图象大致为A.B.C.D.【答案】D【解析】函数过定点,排除,.函数的导数,由得,得或,此时函数单调递增,由得,得或,此时函数单调递减,排除,也可以利用(1),排除,,故选.11.(2017•山东)已知当,时,函数的图象与的图象有且只有一个交点,则正实数的取值范围是A.,,B.,,C.,D.,,【答案】B【解析】根据题意,由于为正数,为二次函数,在区间为减函数,,为增函数,函数为增函数,分2种情况讨论:①、当时,有,在区间,上,为减函数,且其值域为,,函数为增函数,其值域为,,此时两个函数的图象有1个交点,符合题意;②、当时,有,在区间为减函数,,为增函数,函数为增函数,其值域为,,若两个函数的图象有1个交点,则有,解可得或,又由为正数,则;综合可得:的取值范围是,...