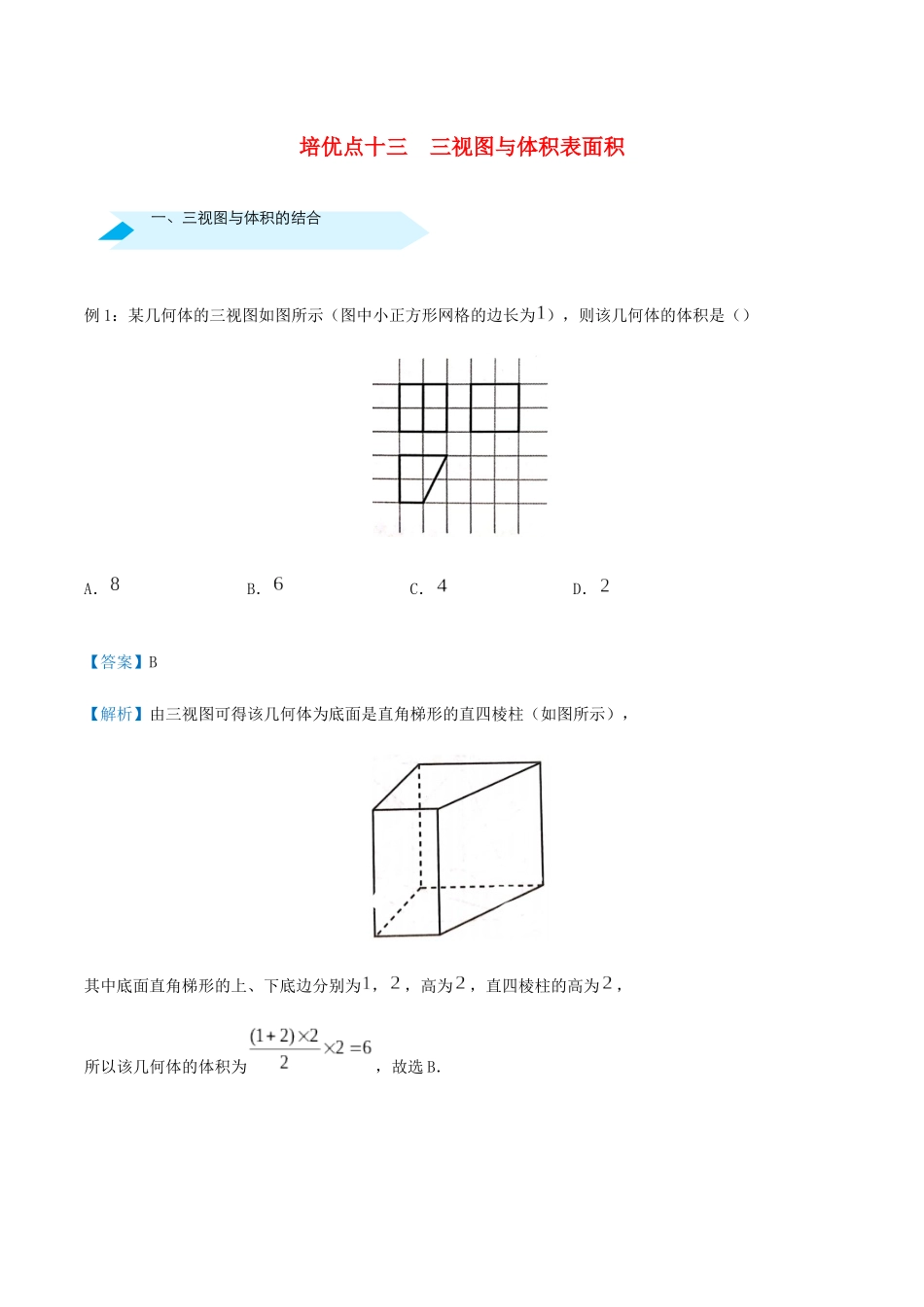
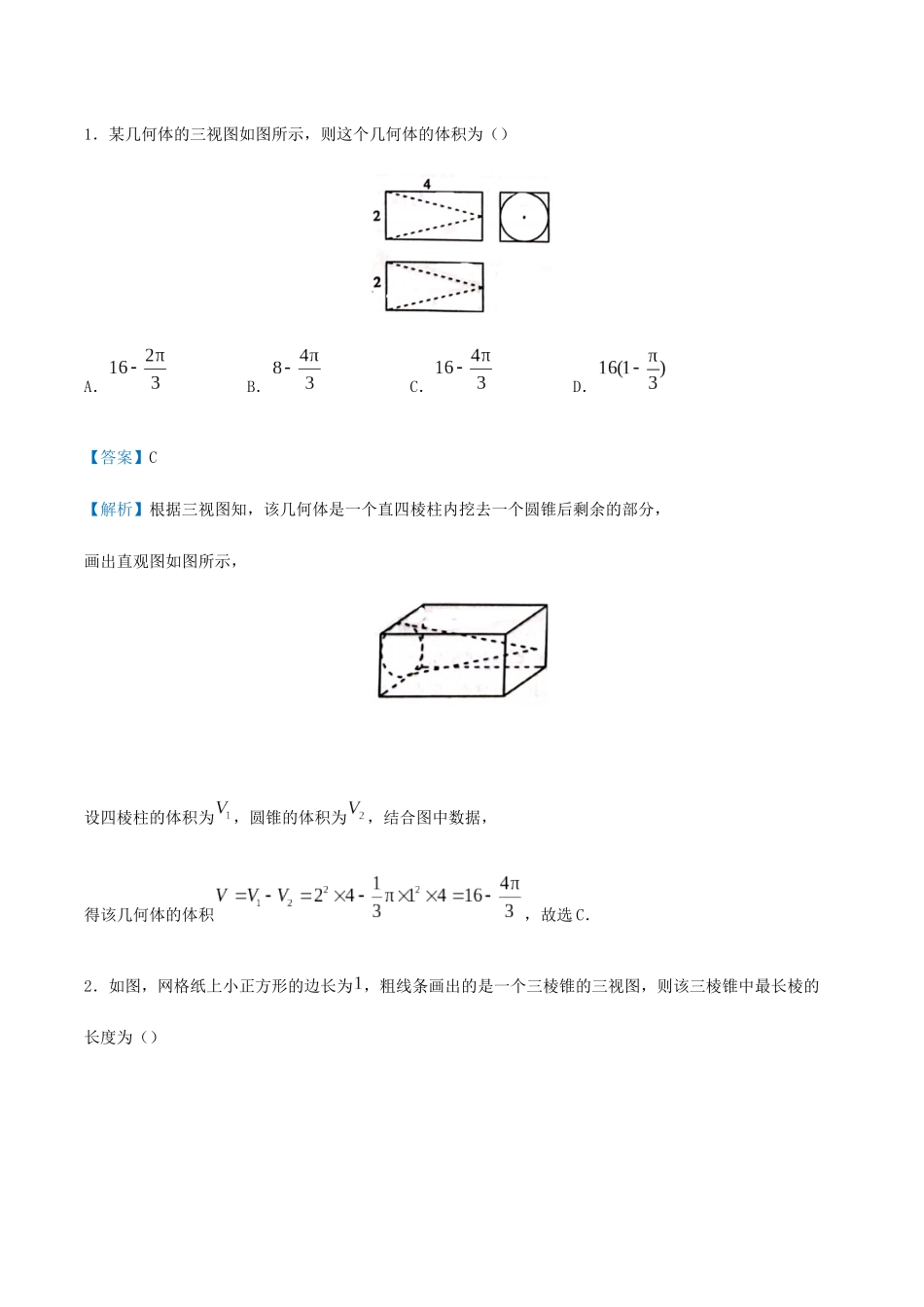
一、三视图与体积的结合培优点十三三视图与体积表面积例1:某几何体的三视图如图所示(图中小正方形网格的边长为),则该几何体的体积是()A.B.C.D.【答案】B【解析】由三视图可得该几何体为底面是直角梯形的直四棱柱(如图所示),其中底面直角梯形的上、下底边分别为,,高为,直四棱柱的高为,所以该几何体的体积为,故选B.二、三视图与表面积的结合对点增分集训例2:如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,其中俯视图由两个半圆和两个线段组成,则该几何体的表面积为()A.B.C.D.【答案】C【解析】由三视图知,该几何体是一个大半圆柱挖去一个小半圆柱得到的,两个半圆柱的底面半径分别为和,高均为,所以该几何体的表面积为.一、选择题1.某几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.【答案】C【解析】根据三视图知,该几何体是一个直四棱柱内挖去一个圆锥后剩余的部分,画出直观图如图所示,设四棱柱的体积为,圆锥的体积为,结合图中数据,得该几何体的体积,故选C.2.如图,网格纸上小正方形的边长为,粗线条画出的是一个三棱锥的三视图,则该三棱锥中最长棱的长度为()A.B.C.D.【答案】D【解析】如图,三棱锥即为所求几何体,根据题设条件,知辅助的正方体棱长为,,,,,,,则最长棱为,长度为.3.古人采取“用臼舂米”的方法脱去稻谷的外壳,获得可供食用的大米,用于舂米的“臼”多用石头或木头制成.一个“臼”的三视图如图所示,则凿去部分(看成一个简单的组合体)的体积为()A.B.C.D.【答案】A【解析】由三视图得凿去部分是圆柱与半球的组合体,其中圆柱的高为,底面圆的半径为,半球的半径为,所以组合体的体积为,故选A.4.某几何体的三视图如图所示,在该几何体的各个面中,面积最小的面与底面的面积的比值为()A.B.C.D.【答案】C【解析】由三视图可知,该几何体是高为的四棱锥,如图所示,记为.易知面积最小的面为左侧面,其面积为.将底面补为梯形,则底面的面积为,所以面积最小的面与底面的面积的比值为,故选C.5.一个几何体的三视图如图所示,其中正视图和俯视图中的四边形是边长为的正方形,则该几何体的表面积为()A.B.C.D.【答案】B【解析】由三视图可知该几何体是一个圆柱体和一个球体的四分之一的组合体,则所求的几何体的表面积为,故选B.6.如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则该几何体的表面积为()A.B.C.D.【答案】D【解析】由三视图可知,该几何体是由底面半径为,高为的半圆柱挖去一个半径为的半球得到的,则该几何体的表面积.故选B.7.某几何体的三视图如图所示,则这个几何体的体积是()A.B.C.D.【答案】C【解析】所求几何体可看作将长方体截去两个三棱柱得到的几何体,在长方体中还原该几何体,如图中所示,长方体的长、宽、高分别为,,,两个三棱柱的高为,底面是两直角边长分别为和的直角三角形,故该几何体的体积,故选C.8.某装饰品的三视图如图所示,则该装饰品的表面积为()A.B.C.D.【答案】C【解析】由装饰品的三视图可知,该装饰品是由一个棱长为的正方体,切去四个四分之一的圆锥所得的几何体,其中圆锥的底面半径为,高为,则该装饰品的表面积为,故选C.9.如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,俯视图中的两条曲线均为圆弧,则该几何体的体积为()A.B.C.D.【答案】C【解析】由三视图知,该几何体是由棱长为的正方体截去一个底面半径为、高为的圆锥和一个底面半径为、高为的圆柱而得到的,所以该几何体的体积,故选C.10.我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为,则对该几何体描述:①四个侧面都是直角三角形;②最长的侧棱长为;③四个侧面中有三个侧面是全等的直角三角形;④外接球的表面积为.其中正确的个数是()A.B.C.D.【答案...