考点测试15导数的应用(一)一、基础小题1.函数f(x)=1+x-sinx在(0,2π)上是()A.增函数B.减函数C.在(0,π)上增,在(π,2π)上减D.在(0,π)上减,在(π,2π)上增答案A解析f′(x)=1-cosx>0,∴f(x)在(0,2π)上递增.2.设函数f(x)=+lnx,则()A.x=为f(x)的极大值点B.x=为f(x)的极小值点C.x=2为f(x)的极大值点D.x=2为f(x)的极小值点答案D解析f(x)=+lnx(x>0),f′(x)=-+=,x>2时,f′(x)>0,这时f(x)为增函数;0
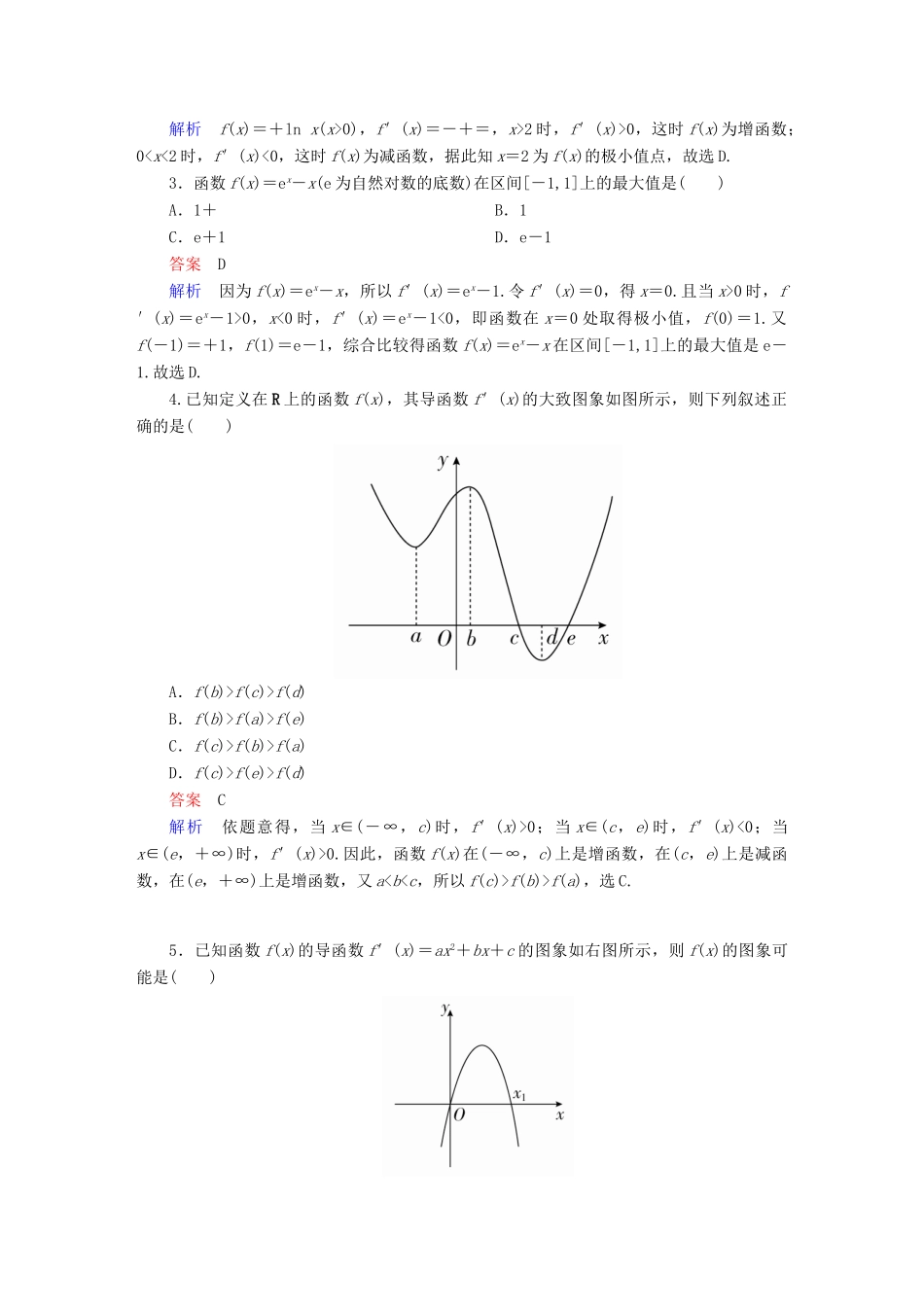
0时,f′(x)=ex-1>0,x<0时,f′(x)=ex-1<0,即函数在x=0处取得极小值,f(0)=1.又f(-1)=+1,f(1)=e-1,综合比较得函数f(x)=ex-x在区间[-1,1]上的最大值是e-1.故选D.4.已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是()A.f(b)>f(c)>f(d)B.f(b)>f(a)>f(e)C.f(c)>f(b)>f(a)D.f(c)>f(e)>f(d)答案C解析依题意得,当x∈(-∞,c)时,f′(x)>0;当x∈(c,e)时,f′(x)<0;当x∈(e,+∞)时,f′(x)>0.因此,函数f(x)在(-∞,c)上是增函数,在(c,e)上是减函数,在(e,+∞)上是增函数,又af(b)>f(a),选C.5.已知函数f(x)的导函数f′(x)=ax2+bx+c的图象如右图所示,则f(x)的图象可能是()答案D解析当x<0时,由导函数f′(x)=ax2+bx+c<0,知相应的函数f(x)在该区间内单调递减;当x>0时,由导函数f′(x)=ax2+bx+c的图象可知,导函数在区间(0,x1)内的值是大于0的,则在此区间内函数f(x)单调递增.只有D选项符合题意.6.已知函数f(x)=-x3+ax2-x-1在R上是单调函数,则实数a的取值范围是()A.(-∞,-)∪[,+∞)B.[-,]C.(-∞,-)∪(,+∞)D.(-,)答案B解析f′(x)=-3x2+2ax-1≤0恒成立,∴Δ=4a2-12≤0,-≤a≤.7.若函数f(x)=-x2+x+1在区间上有极值点,则实数a的取值范围是()A.B.C.D.答案C解析 f(x)=-x2+x+1,∴f′(x)=x2-ax+1.若函数f(x)=-x2+x+1在区间上有极值点,则f′(x)=x2-ax+1在区间内有零点,由f′(x)=x2-ax+1=0,可知a=x+. 函数y=x+在上单调递减,在(1,3)上单调递增,∴y∈,即2≤a<.当a=2时,由f′(x)=0解得x=1,而f(x)在,(1,3)上单调性相同,故不存在极值点,则a≠2.综上可知,21,则不等式ex·f(x)>ex+1的解集为()A.{x|x>0}B.{x|x<0}C.{x|x<-1或x>1}D.{x|x<-1或0ex-ex=0,所以g(x)=ex·f(x)-ex为R上的增函数,又因为g(0)=e0·f(0)-e0=1,所以原不等式转化为g(x)>g(0),解得x>0.二、高考小题9.[2016·全国卷Ⅰ]若函数f(x)=x-sin2x+asinx在(-∞,+∞)单调递增,则a的取值范围是()A.[-1,1]B.[-1,]C.D.答案C解析函数f(x)=x-sin2x+asinx在(-∞,+∞)单调递增,等价于f′(x)=1-cos2x+acosx=-cos2x+acosx+≥0在(-∞,+∞)恒成立.设cosx=t,则g(t)=-t2+at+≥0在[-1,1]恒成立,所以解得-≤a≤.故选C.10.[2015·全国卷Ⅱ]设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是()A.(-∞,-1)∪(0,1)B.(-1,0)∪(1,+∞)C.(-∞,-1)∪(-1,0)D.(0,1)∪(1,+∞)答案A解析令g(x)=(x≠0),则g′(x)=,由题意知,当x>0时,g′(x)<0,∴g(x)在(0,+∞)上是减函数. f(x)是奇函数,f(-1)=0,∴f(1)=-f(-1)=0,∴g(1)==0,∴当x∈(0,1)时,g(x)>0,从而f(x)>0;当x∈(1,+∞)时,g(x)<0,从而f(x)<0.又 g(-x)====g(x),∴g(x)是偶函数,∴当x∈(-∞,-1)时,g(x)<0,从而f(x)>0;当x∈(-1,0)时,g(x)>0,从而f(x)<0.综上,所求x的取值范围是(-∞...