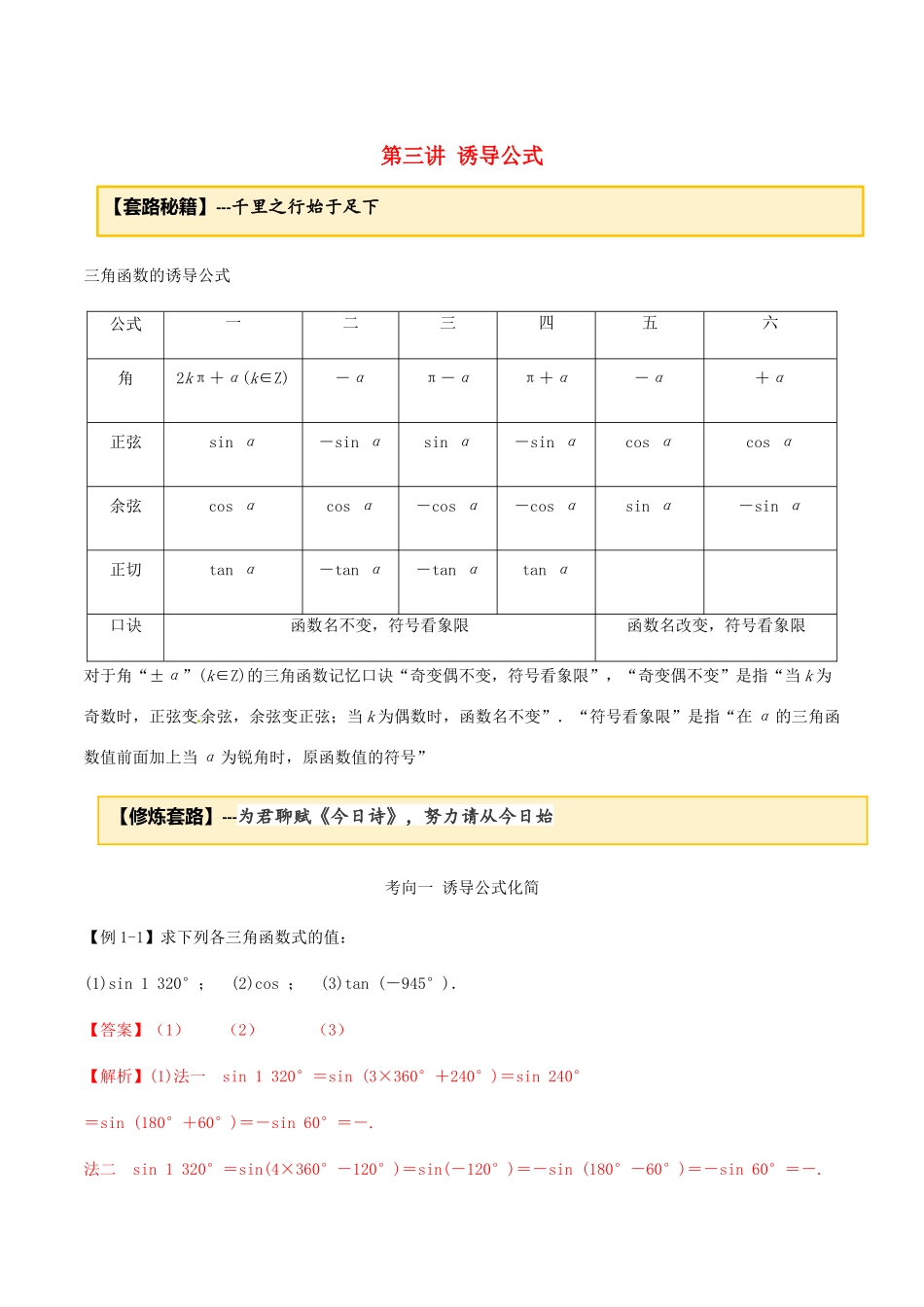
第三讲诱导公式三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)-απ-απ+α-α+α正弦sinα-sinαsinα-sinαcosαcosα余弦cosαcosα-cosα-cosαsinα-sinα正切tanα-tanα-tanαtanα口诀函数名不变,符号看象限函数名改变,符号看象限对于角“±α”(k∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,“奇变偶不变”是指“当k为奇数时,正弦变余弦,余弦变正弦;当k为偶数时,函数名不变”.“符号看象限”是指“在α的三角函数值前面加上当α为锐角时,原函数值的符号”【修炼套路】---为君聊赋《今日诗》,努力请从今日始考向一诱导公式化简【例1-1】求下列各三角函数式的值:(1)sin1320°;(2)cos;(3)tan(-945°).【答案】(1)(2)(3)【解析】(1)法一sin1320°=sin(3×360°+240°)=sin240°=sin(180°+60°)=-sin60°=-.法二sin1320°=sin(4×360°-120°)=sin(-120°)=-sin(180°-60°)=-sin60°=-.【套路秘籍】---千里之行始于足下(2)法一cos=cos=cos=cos(π+)=-cos=-.法二cos=cos=cos=-cos=-.(3)tan(-945°)=-tan945°=-tan(225°+2×360°)=-tan225°=-tan(180°+45°)=-tan45°=-1.【例1-2】化简·sin(α-π)·cos(2π-α)的结果为.【答案】-sin2α【解析】原式=·(-sinα)·cosα=-sin2α.【套路总结】(1)诱导公式的两个应用①求值:负化正,大化小,化到锐角为终了.②化简:统一角,统一名,同角名少为终了.(2)含2π整数倍的诱导公式的应用1.已知α为锐角,cos=,则cos(π+α)=.【答案】-【解析】 cos=sinα=,且α为锐角,∴cosα=,∴cos(π+α)=-cosα=-.2.化简:=.【答案】-1【解析】原式====-=-·=-1.3.计算:(1)sin(-)-cos(-);(2)7cos270°+3sin270°+tan765°;(3)cos(-120°)sin(-150°)+tan855°.【答案】(1)1(2)-2(3)-【解析】(1)原式=-sin(4π+)-cos(2π+)=-sin(π+)-cos(π+)=sin+cos=+=1.(2)原式=7cos(180°+90°)+3sin(180°+90°)+tan(2×360°+45°)=-7cos90°-3sin90°+tan45°=0-3+1=-2.(3)原式=cos120°(-sin150°)+tan855°=-cos(180°-60°)sin(180°-30°)+tan(135°+2×360°)=-(-cos60°)sin30°+tan135°=-(-cos60°)sin30°+tan(180°-45°)=-(-cos60°)sin30°-tan45°=×-1=-.考向二诱导公式与定义同角综合【例2】(1)已知cosα=,-<α<0,则的值为.(2)已知角θ的顶点在坐标原点,始边与x轴非负半轴重合,终边在直线3x-y=0上,则=.(3)已知f(α)=(sinα≠0,1+2sinα≠0),则f=.【答案】(1)(2)(3)【解析】(1) -<α<0,∴sinα=-=-,∴tanα=-2.则==-==.(2)由已知得tanθ=3,∴===.(3) f(α)====,∴f====.考向三凑角【例3】(1)已知sin=,则cos的值为()A.B.-C.-D.(2)已知,求的值.(3)已知cos(α-75°)=,且α为第四象限角,求sin(105°+α)的值.【答案】(1)B(2)(3)【解析】(1)因为sin=,所以cos=cos=-sin=-。(2)cos=cos=sin=.(3) cos(α-75°)=-<0,且α为第四象限角,∴α-75°是第三象限角.∴sin(α-75°)=-=-=-.∴sin(105°+α)=sin[180°+(α-75°)]=-sin(α-75°)=.【套路总结】巧用相关角的关系能简化解题的过程.常见的互余关系有与,与,与等;【举一反三】1.已知sin(π6−x)=12,则sin(7π6−x)+sin2(π3+x)=¿¿A.14B.34C.−14D.−12【答案】A【解析】 已知sin(π6−x)=12,则sin(7π6−x)+sin2(π3+x)=−sin(π6−x)+1−cos2(π3+x)¿−12+1−sin2(π6−x)=12−¿,故选:A.2.已知,则的值等于()A.B.C.D.【答案】D【解析】 +α-=,∴cos=cos=-sin=-.故选D.3.已知sin=,求cos的值.【答案】【解析】 +α+-α=,∴-α=-.∴cos=cos=sin=.4.已知cos=,求cos·sin的值.【答案】-【解析】cos·sin=cos·sin=-cos·sin=-sin=-cos=-.【运用套路】---纸上得来终觉浅,...