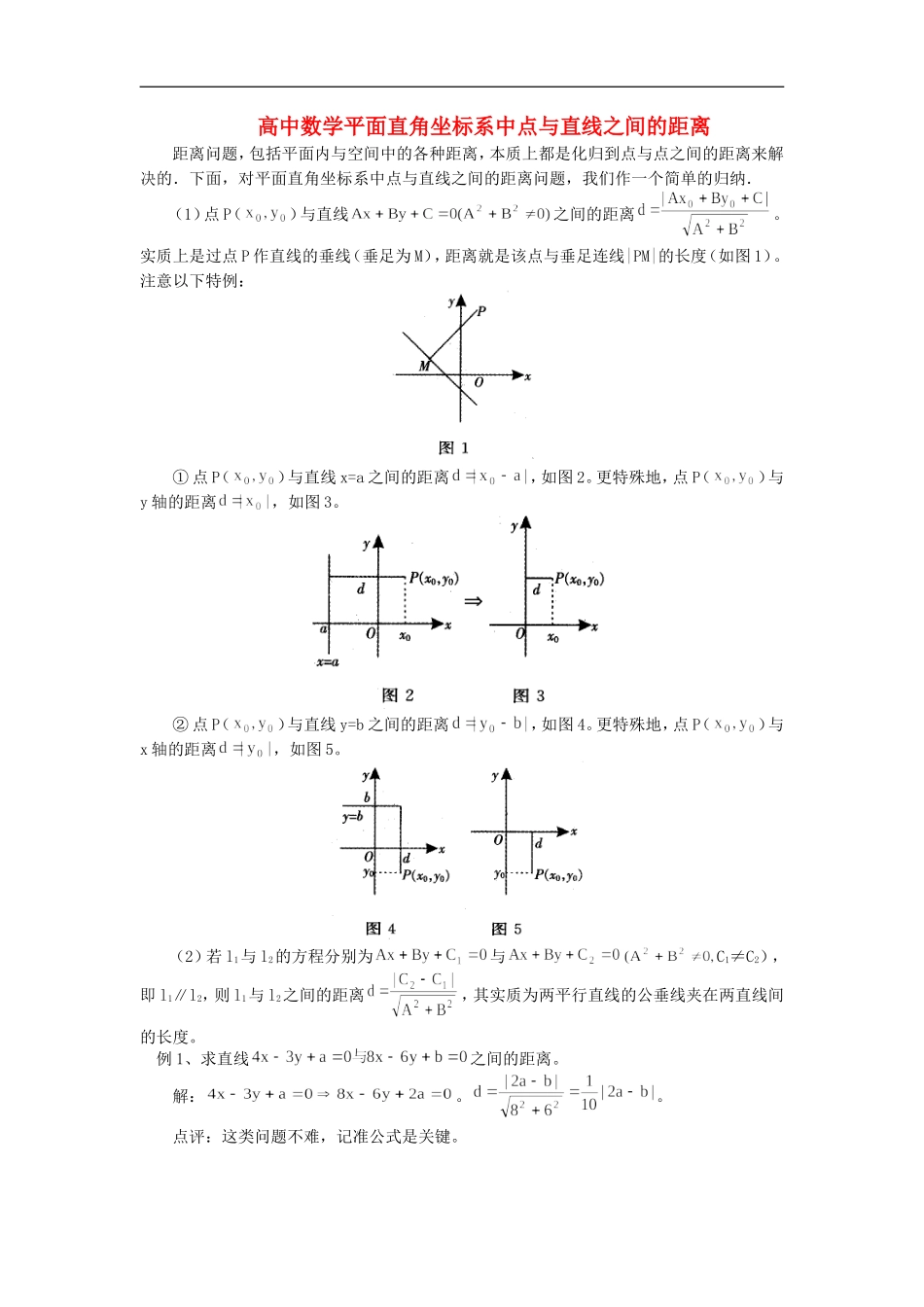
高中数学平面直角坐标系中点与直线之间的距离距离问题,包括平面内与空间中的各种距离,本质上都是化归到点与点之间的距离来解决的.下面,对平面直角坐标系中点与直线之间的距离问题,我们作一个简单的归纳.(1)点P()与直线之间的距离。实质上是过点P作直线的垂线(垂足为M),距离就是该点与垂足连线|PM|的长度(如图1)。注意以下特例:①点P()与直线x=a之间的距离,如图2。更特殊地,点P()与y轴的距离,如图3。②点P()与直线y=b之间的距离,如图4。更特殊地,点P()与x轴的距离,如图5。(2)若l1与l2的方程分别为与C1≠C2),即l1∥l2,则l1与l2之间的距离,其实质为两平行直线的公垂线夹在两直线间的长度。例1、求直线之间的距离。解:。。点评:这类问题不难,记准公式是关键。例2、已知点()到直线的距离为,且,求。解:直线方程化为,由点线距离公式得:。∵,∴。点评:由点到直线距离公式入手,注意到角的范围,去掉绝对值符号,转化为关于sin的一元二次方程,问题得到解决.例3、求过点A(3,5),且与原点距离最远的直线方程.解:如图6所示,l是过点A(3,5)且垂直于OA的直线,l′是过点A(3,5)的任意直线,原点O与l,l′的距离分别为OA,OA′。由直角三角形的三边关系知,所以,直线l就是满足条件的直线。,由直线方程的点斜式得,即。点评:解析几何研究的本质就是数形结合.本题若引入斜率k作为参数写出直线方程,然后写出距离的表达式,则问题转化为函数的最值问题,思路自然,但不易得解.所以,公式也不是万能的,解这类题时要有数形结合的意识.例4、求过点P(-1,2)且与点A(2,3)和B(-4,5)距离相等的直线方程。解:①当所求直线的斜率不存在时,过点P(-1,2)的直线方程为,与点A(2,3)的距离,与点B(-4,5)的距离,题设被满足。②当所求直线的斜率存在时,设所求直线的方程为,即,依题意得,,所以所求方程为,即。综上,满足条件的直线方程为或点评:本题再次表明,必须熟记公式.本题还提示我们:凡涉及到直线的斜率时,一定要对斜率是否存在(斜率不存在不等于直线不存在)进行讨论,否则就会对而不全.(责任编辑徐利杰)