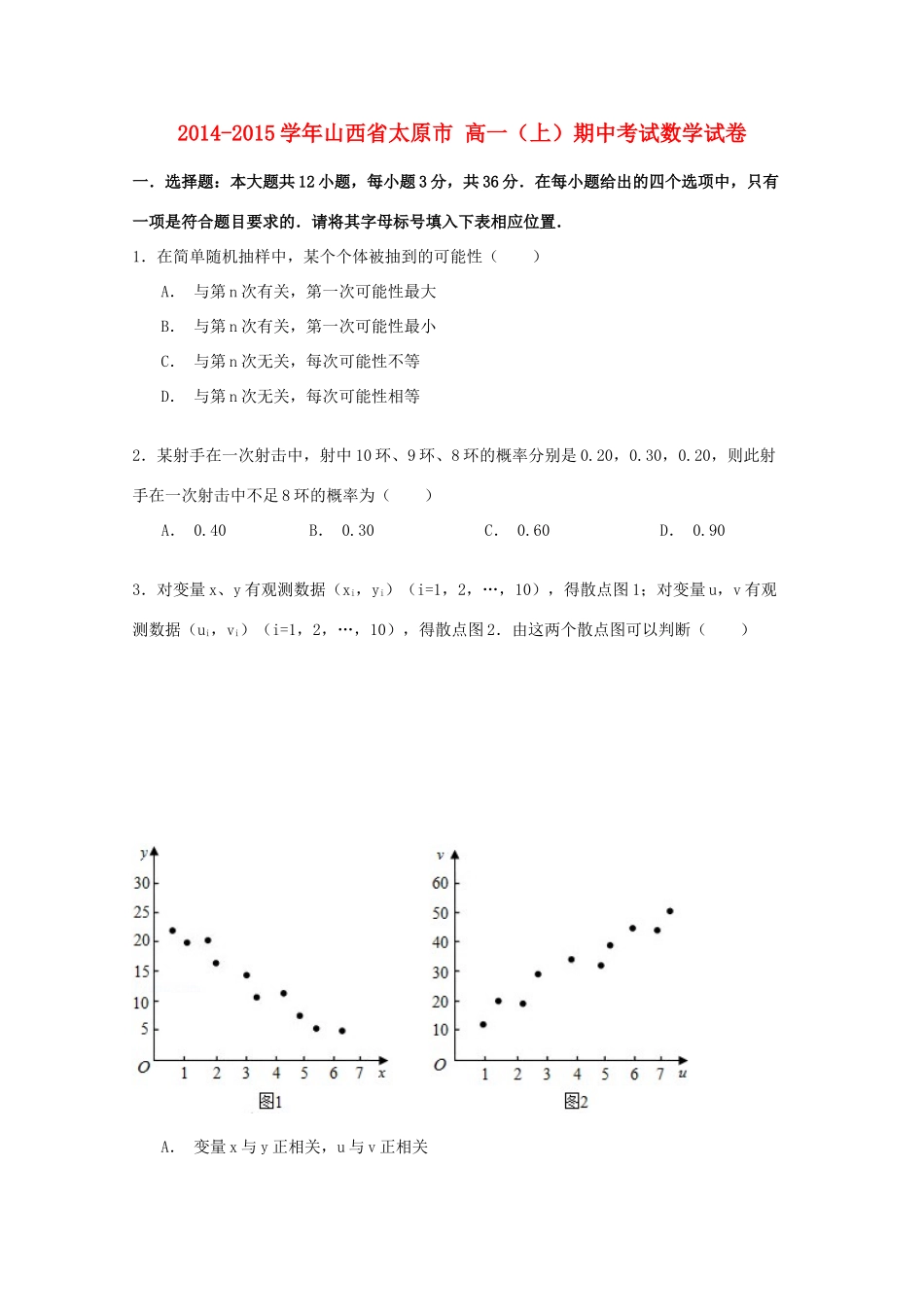
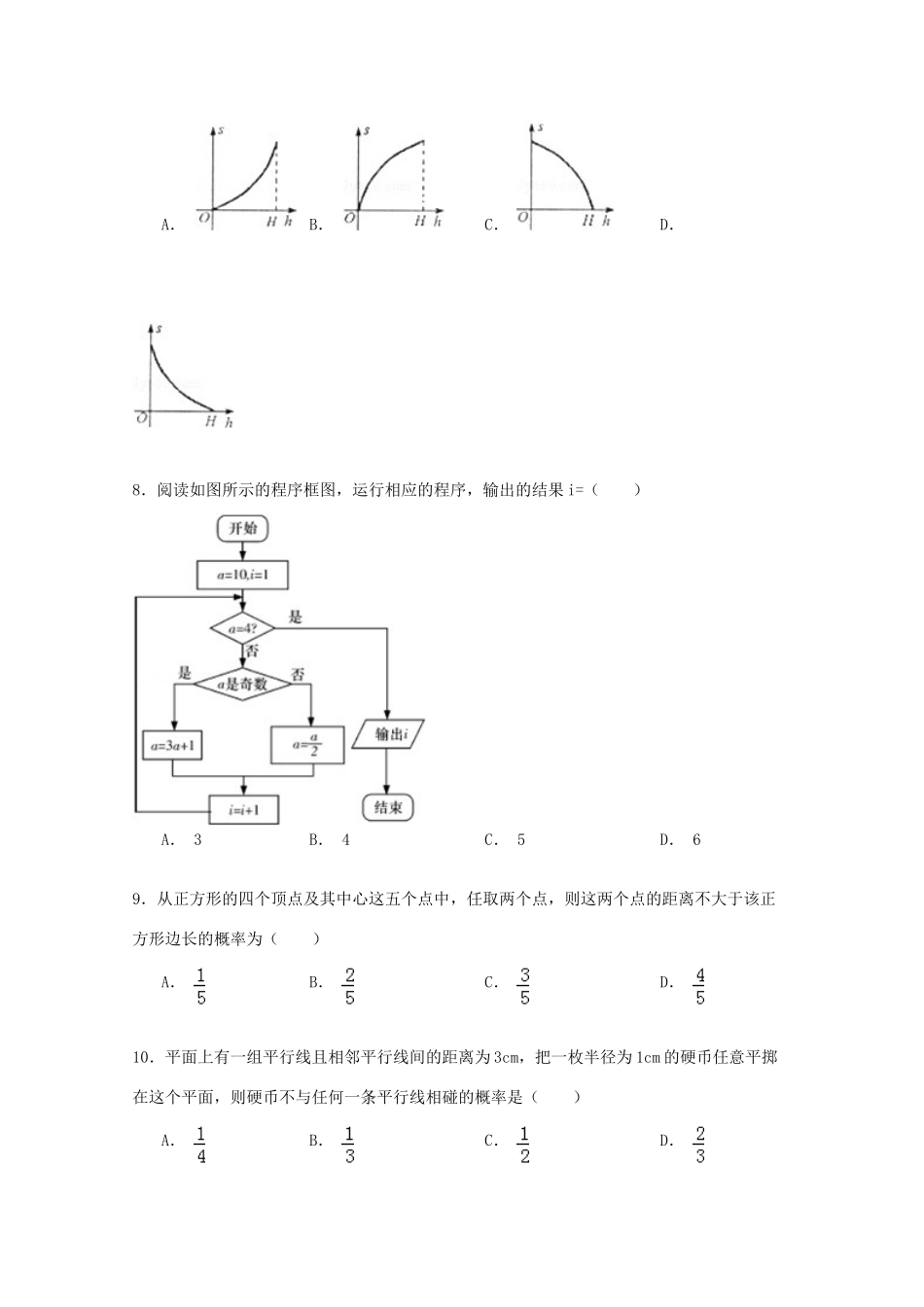
2014-2015学年山西省太原市高一(上)期中考试数学试卷一.选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将其字母标号填入下表相应位置.1.在简单随机抽样中,某个个体被抽到的可能性()A.与第n次有关,第一次可能性最大B.与第n次有关,第一次可能性最小C.与第n次无关,每次可能性不等D.与第n次无关,每次可能性相等2.某射手在一次射击中,射中10环、9环、8环的概率分别是0.20,0.30,0.20,则此射手在一次射击中不足8环的概率为()A.0.40B.0.30C.0.60D.0.903.对变量x、y有观测数据(xi,yi)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(i=1,2,…,10),得散点图2.由这两个散点图可以判断()A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关4.以下各数可能是五进制数的为()A.55B.106C.732D.21345.读如图程序,当输入的x为60时,输出y的值为()A.30B.31C.36D.616.某班共有52人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、29号、42号同学在样本中,那么样本中还有一个同学的学号是()A.10B.11C.12D.167.如图,平面图形中阴影部分面积S是h(h∈)的函数,则该函数的图象大致是()A.B.C.D.8.阅读如图所示的程序框图,运行相应的程序,输出的结果i=()A.3B.4C.5D.69.从正方形的四个顶点及其中心这五个点中,任取两个点,则这两个点的距离不大于该正方形边长的概率为()A.B.C.D.10.平面上有一组平行线且相邻平行线间的距离为3cm,把一枚半径为1cm的硬币任意平掷在这个平面,则硬币不与任何一条平行线相碰的概率是()A.B.C.D.11.随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p1,点数之和大于5的概率记为p2,点数之和为偶数的概率记为p3,则()A.p1<p2<p3B.p2<p1<p3C.p1<p3<p2D.p3<p1<p212.已知x与y之间的几组数据如下表:x123456y021334假设根据上表数据所得线性回归直线方程为.若某同学根据上表中前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是()A.B.C.D.二、填空题:本大题共4个小题,每小题3分,共12分,把答案填在横线上.13.如图所示的矩形长为20,宽为10.在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为.14.用秦九韶算法求多项式:f(x)=1+x+2x2+3x3+4x4+5x5+7x7在x=2的值时,v3的值为.15.从0,1,2,3,4,5,6中任取五个不同的数,则这五个数的中位数是4的概率为.16.把下面求2﹣22+23﹣24+…﹣210的程序语言补充完整.三、解答题:本大题共4小题,共52分.解答应写出文字说明、证明过程或演算步骤.17.用辗转相除法求228和123的最大公约数.18.某公司20名员工年龄数据如下表:年龄(岁)员工数(人)191283293305314323401合计20(1)求这20名员工年龄的众数与极差;(2)以十位数为茎,个位数为叶,作出这20名员工年龄的茎叶图.19.某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:(a,b),(a,),(a,b),(,b),(,),(a,b),(a,b),(a,),(,b),(a,),(,),(a,b),(a,),(,b)(a,b)其中a,分别表示甲组研发成功和失败,b,分别表示乙组研发成功和失败.(Ⅰ)若某组成功研发一种新产品,则给该组记1分,否则记0分,试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;(Ⅱ)若该企业安排甲、乙两组各自研发一样的产品,试估计恰有一组研发成功的概率.20.在某幼儿园的美术课上,老师带领小朋友用水彩笔为本子上两个大小不同的气球涂色,要求一个气球只涂一种颜色,两个气球分别涂不同的颜色.小朋友豆豆可用的有暖色系水彩笔红色、橙色各一支,冷色系水彩笔绿色、蓝色、紫色各一支.(1)豆豆从他可用的五支水彩笔中随机取出两支按老师要求给气球涂色,求两...