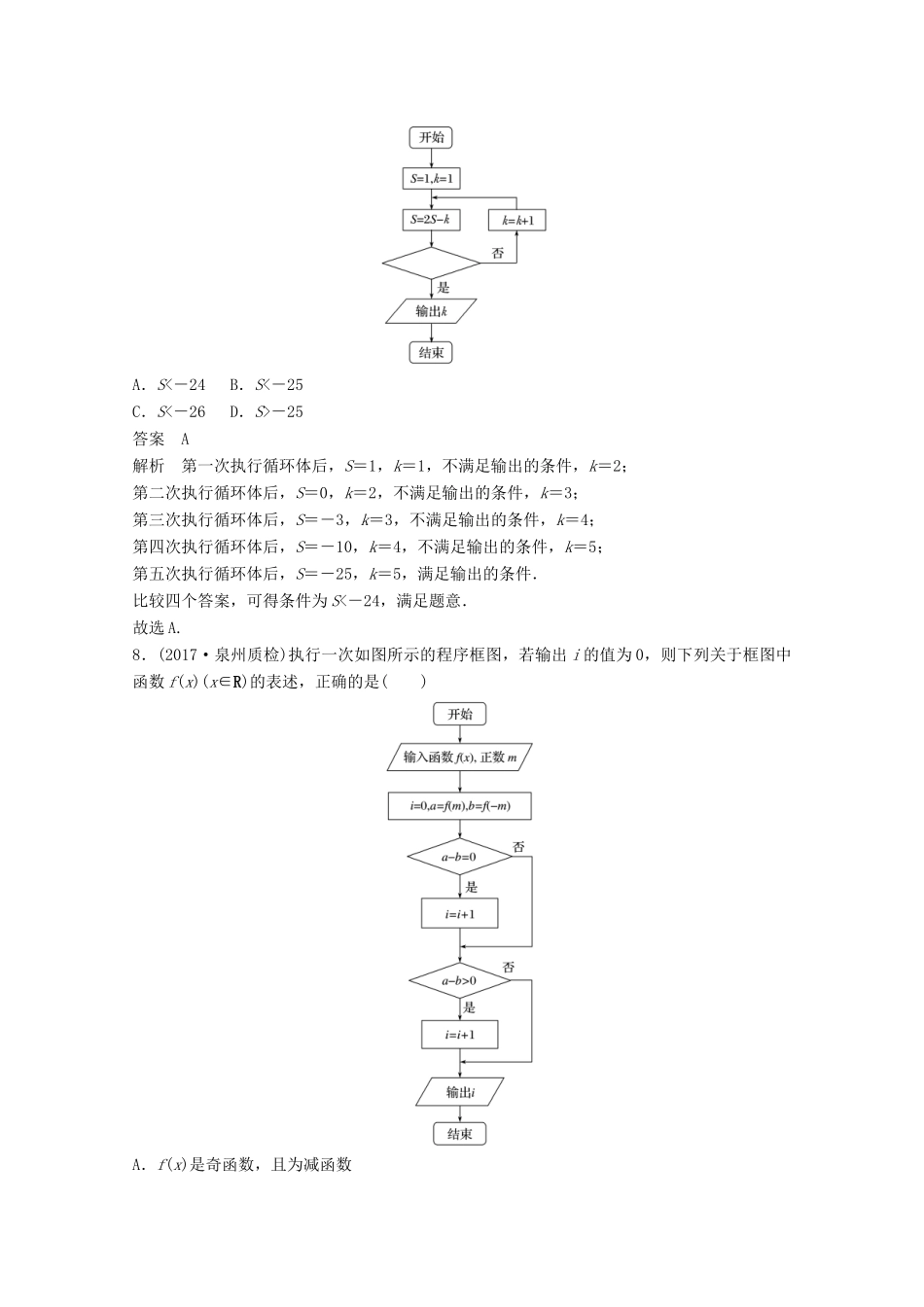
12+4分项练14算法与复数1.(2017·全国Ⅱ)(1+i)(2+i)等于()A.1-iB.1+3iC.3+iD.3+3i答案B解析(1+i)(2+i)=2+i+2i-1=1+3i.故选B.2.(2017届福建省厦门外国语学校适应性考试)复数z=+i5的共轭复数为()A.1-2iB.1+2iC.i-1D.1-i答案A解析根据题意化简得z=1+2i,=1-2i,故选A.3.(2017届安徽省蚌埠市质检)复数(a-i)(1-i)(a∈R)的实部与虚部相等,则实数a等于()A.-1B.0C.1D.2答案B解析由题意可得(a-i)(1-i)=a-i-ai+i2=(a-1)-(a+1)i,结合题意可知,a-1=-a-1,解得a=0.故选B.4.(2017·全国Ⅲ)复平面内表示复数z=i(-2+i)的点位于()A.第一象限B.第二象限C.第三象限D.第四象限答案C解析 z=i(-2+i)=-1-2i,∴复数z=-1-2i所对应的复平面内的点为Z(-1,-2),位于第三象限.故选C.5.如图,在复平面内,复数z1和z2对应的点分别是A和B,则等于()A.+iB.+iC.--iD.--i答案D解析由题图得z1=-2-i,z2=i,所以===--i,故选D.6.(2017·辽宁省实验中学模拟)某程序框图如图所示,若输入的n=10,则输出的结果为()A.B.C.D.答案C解析初始值:S=0,k=1,k<10k=2,S=0+1-,k=3,S=0+1-+,…,k=9,S=0+1-++…+,k=10,S=0+1-++…++=.故选C.7.(2017届辽宁省锦州市质检)阅读如图的程序框图,如果输出k=5,那么空白的判断框中应填入的条件是()A.S<-24B.S<-25C.S<-26D.S>-25答案A解析第一次执行循环体后,S=1,k=1,不满足输出的条件,k=2;第二次执行循环体后,S=0,k=2,不满足输出的条件,k=3;第三次执行循环体后,S=-3,k=3,不满足输出的条件,k=4;第四次执行循环体后,S=-10,k=4,不满足输出的条件,k=5;第五次执行循环体后,S=-25,k=5,满足输出的条件.比较四个答案,可得条件为S<-24,满足题意.故选A.8.(2017·泉州质检)执行一次如图所示的程序框图,若输出i的值为0,则下列关于框图中函数f(x)(x∈R)的表述,正确的是()A.f(x)是奇函数,且为减函数B.f(x)是偶函数,且为增函数C.f(x)不是奇函数,也不为减函数D.f(x)不是偶函数,也不为增函数答案D解析因为输出i=0,根据框图,应该有a-b≠0,a-b≤0,即f(m)≠f(-m),f(m)≤f(-m),又m>-m,所以函数不是偶函数,也不是增函数,故选D.9.(2017届福建省厦门第一中学模拟)运行如图所示的程序框图,则输出结果为()A.2017B.2016C.1009D.1008答案D解析输出结果为S=0-1+2-3+4-…+2016=1008,故选D.10.(2017届陕西省渭南市二模)公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“微率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为(参考数据:≈1.414,≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)()A.12B.36C.24D.48答案C解析模拟执行程序,可得n=6,S=3sin60°=,不满足条件;n=12,S=6sin30°=3,不满足条件;n=24,S=12sin15°=12×0.2588=3.1056,满足条件S≥3.10,退出循环,输出n的值为24.故选C.11.(2017届辽宁省锦州市质检)执行如图所示的程序框图,则输出i的值为()A.1006B.1007C.1008D.1009答案D解析n=1,r=0,s=1,r+s=1,i=1,1<2017;n=2,r=-1,s=0,r+s≠1;n=3,r=0,s=-1,r+s≠1;n=4,r=1,s=0,r+s=1,i=2,4<2017,上述循环为一个周期,且i表示r+s=1出现的次数,一个周期出现2次.当n=2017时结束循环,2017=504×4+1,所以i=504×2+1=1009.故选D.12.(2017届湖北省襄阳市第四中学适应性考试)《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷,卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数...