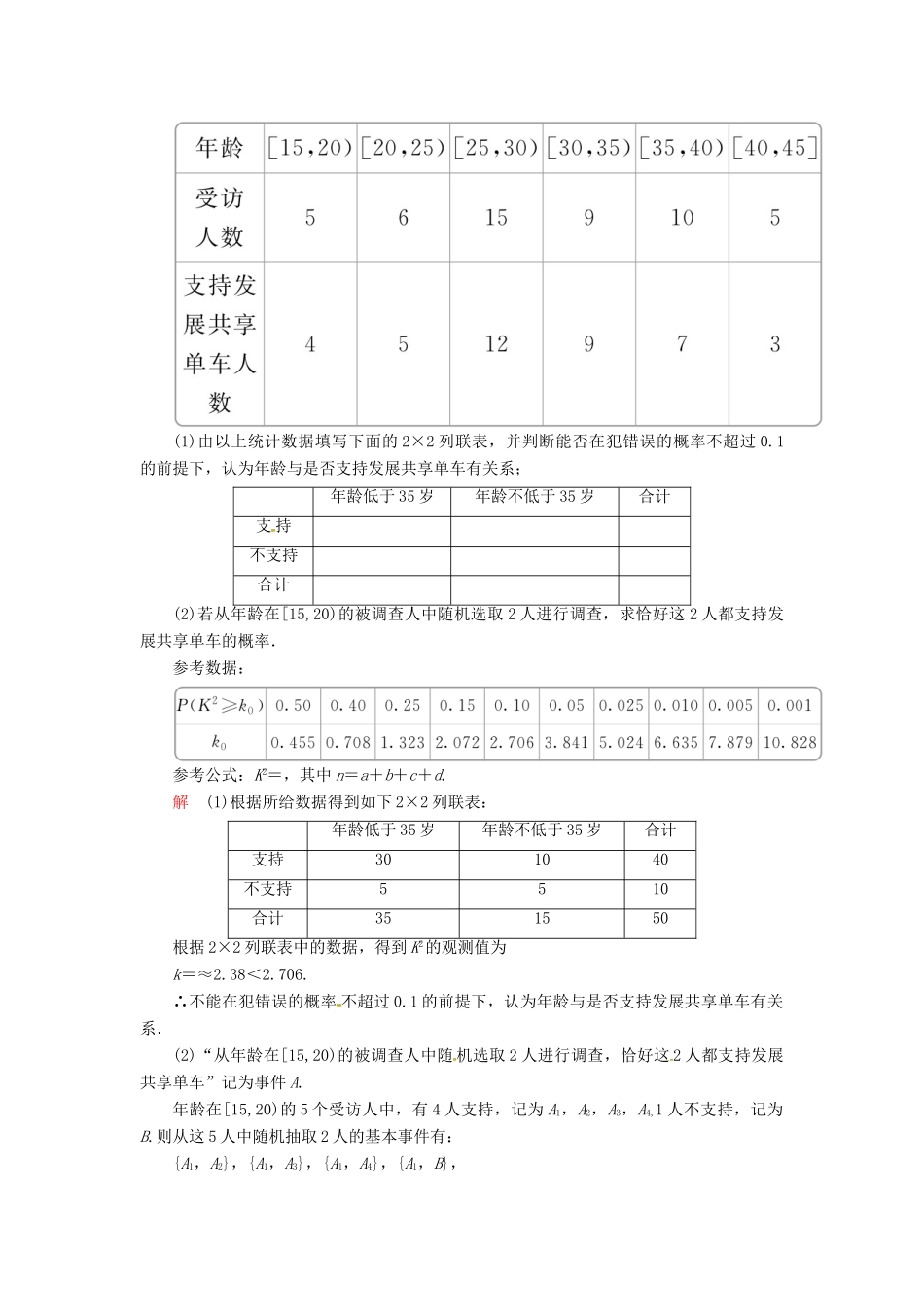
中难提分突破特训(三)1.已知函数f(x)=2sinxsin.(1)求函数f(x)的单调递增区间;(2)锐角△ABC的角A,B,C所对的边分别是a,b,c,角A的平分线交BC于D,直线x=A是函数f(x)图象的一条对称轴,AD=BD=2,求边a.解(1)∵f(x)=2sinxsin,∴f(x)=2sinxsinx·+2sinxcosx·=+sin2x=sin2x-cos2x+=sin+.令-+2kπ≤2x-≤+2kπ,k∈Z,得-+kπ≤x≤+kπ,k∈Z.即函数f(x)的单调递增区间为,k∈Z.(2)∵x=A是函数f(x)图象的一条对称轴,∴2A-=+kπ,k∈Z.∴A=+,k∈Z.又∵△ABC是锐角三角形,∴A=.在△ABD中,∠BAD=,BD=,AD=2,由正弦定理,得=,∴sinB=.∴∠B=.∴∠C=π--=.∠CDA=+=.∴AC=AD=2.在△ABC中,由正弦定理,得=,∴BC=a=.2.近几年,成都街头开始兴起“mobike”“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:(1)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;年龄低于35岁年龄不低于35岁合计支持不支持合计(2)若从年龄在[15,20)的被调查人中随机选取2人进行调查,求恰好这2人都支持发展共享单车的概率.参考数据:参考公式:K2=,其中n=a+b+c+d.解(1)根据所给数据得到如下2×2列联表:年龄低于35岁年龄不低于35岁合计支持301040不支持5510合计351550根据2×2列联表中的数据,得到K2的观测值为k=≈2.38<2.706.∴不能在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系.(2)“从年龄在[15,20)的被调查人中随机选取2人进行调查,恰好这2人都支持发展共享单车”记为事件A.年龄在[15,20)的5个受访人中,有4人支持,记为A1,A2,A3,A4,1人不支持,记为B.则从这5人中随机抽取2人的基本事件有:{A1,A2},{A1,A3},{A1,A4},{A1,B},{A2,A3},{A2,A4},{A2,B},{A3,A4},{A3,B},{A4,B},共10个.其中,恰好抽取的2人都支持发展共享单车的基本事件包含{A1,A2},{A1,A3},{A1,A4},{A2,A3},{A2,A4},{A3,A4},共6个.∴P(A)==.∴从年龄在[15,20)的被调查人中随机选取2人进行调查,恰好这2人都支持发展共享单车的概率是.3.已知四棱锥P-ABCD中,平面PAD⊥平面ABCD,E,F分别为AD,PC上的点,AD=3AE,PC=3PF,四边形BCDE为矩形.(1)求证:PA∥平面BEF;(2)若∠PAD=60°,PA=2AE=2,PB=2,求三棱锥P-BEF的体积.解(1)证明:如图,连接AC,交BE于点M,连接FM.因为四边形BCDE是矩形,所以BC∥DE,BC=DE,所以△AME∽△CMB,所以==.依题意,=,所以==,所以PA∥FM,因为FM⊂平面BEF,PA⊄平面BEF,所以PA∥平面BEF.(2)因为AP=2,AE=1,∠PAD=60°,由余弦定理可得PE=,所以PE⊥AD.又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PE⊂平面PAD,所以PE⊥平面ABCD,所以PE⊥CB.又BE⊥CB,且PE∩BE=E,所以CB⊥平面PEB,而BC=DE=2AE=2,所以点F到平面PEB的距离为,又在直角三角形PEB中,EB==3,所以VP-BEF=VF-PEB=×××3×=.4.在平面直角坐标系xOy中,曲线C的参数方程为(θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.(1)求C的极坐标方程;(2)若直线l1,l2的极坐标方程分别为θ=(ρ∈R),θ=(ρ∈R),设直线l1,l2与曲线C的交点为O,M,N,求△OMN的面积.解(1)由参数方程(θ为参数),得普通方程为x2+(y-2)2=4,所以C的极坐标方程为ρ2cos2θ+ρ2sin2θ-4ρsinθ=0,即ρ=4sinθ.(2)不妨设直线l1:θ=(ρ∈R)与曲线C的交点为O,M,则ρM=|OM|=4sin=2,又直线l2:θ=(ρ∈R)与曲线C的交点为O,N,则ρN=|ON|=4sin=2.又∠MON=,所以S△OMN=|OM|·|ON|=×2×2=2.5.设函数f(x)=+|x-2m|(m>0).(1)求证:f(x)≥8恒成立;(2)求使得不等式f(1)>10成立的实数m的取值范围.解(1)证明:由m>0,有f(x)=+|x-2m|≥==+2m≥2=8,当且仅当=2m,即m=2时取等号.所以f(x)≥8恒成立.(2)f(1)=+|1-2m|(m>0),当1-2m<0,即m>时,f(1)=1+-(1-2m)=+2m,由f(1)>10,得+2m>10,化简得m2-5m+4>0,解得m<1或m>4,所以4,当1-2m≥0,即010,得2+-2m>10,此式在010时,实数m的取值范围是(0,1)∪(4,+∞).