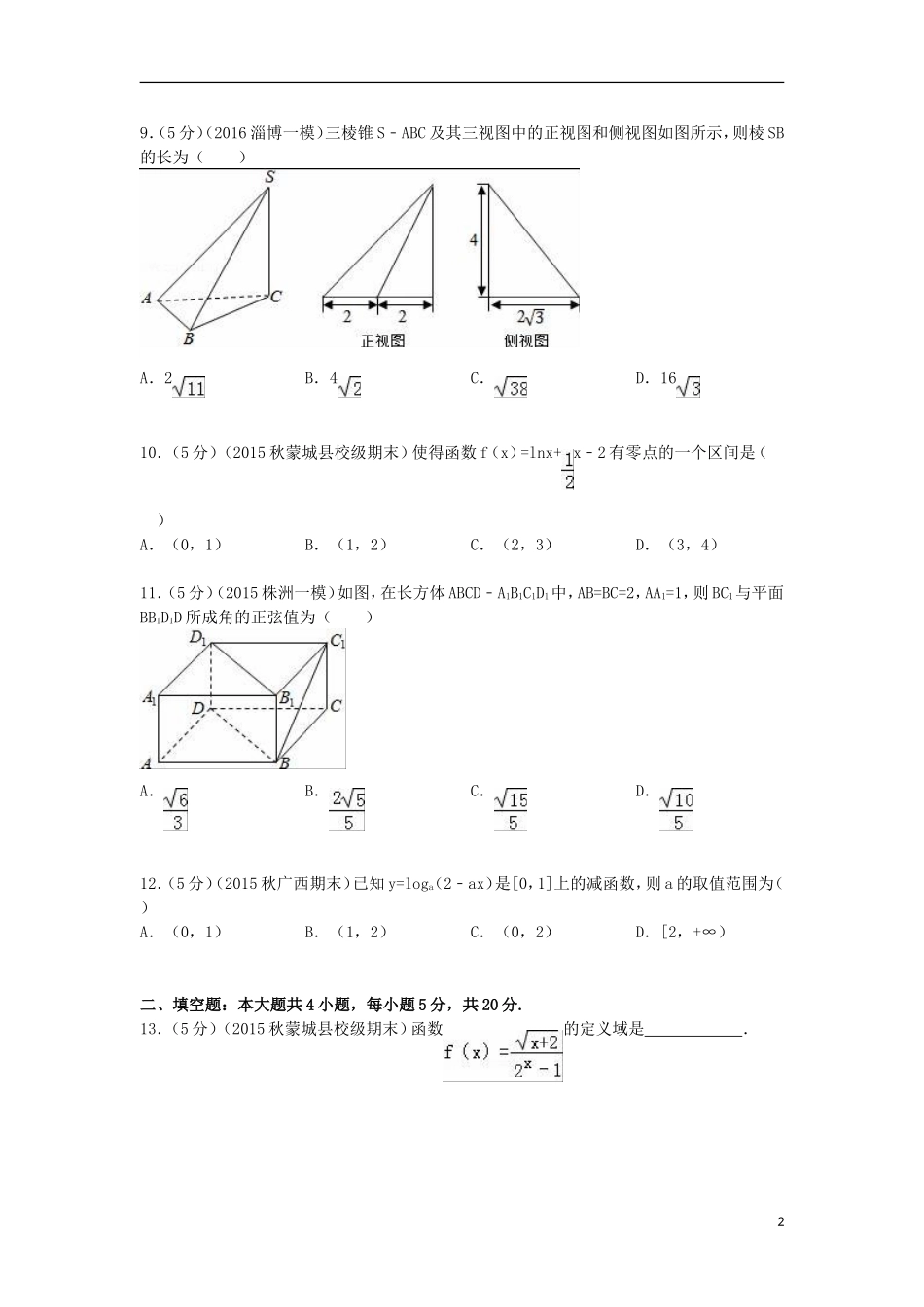
2015-2016学年湖南省邵阳市洞口一中高一(上)期末数学试卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题列出的四个选项中,只有一项是符合题目要求的.1.函数y=ax+2(a>0且a≠1)图象一定过点()A.C.2.已知两圆C1:x2+y2=1,C2:(x﹣3)2+(y﹣4)2=16,则这两圆的位置关系是()A.相交B.外切C.内含D.内切3.设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是()A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β4.下列直线中与直线2x+y+1=0垂直的一条是()A.2x﹣y﹣1=0B.x﹣2y+1=0C.x+2y+1=0D.x+y﹣1=05.在空间坐标中,点B是A(1,2,3)在yOz坐标平面内的射影,O为坐标原点,则|OB|等于()A.B.C.D.6.下列函数是偶函数的是()A.y=x2,x∈[0,1]B.y=x3C.y=2x2﹣3D.y=x7.设全集U=R,集合M={x|y=},N={y|y=3﹣2x},则图中阴影部分表示的集合是()A.{x|<x≤3}B.{x|<x<3}C.{x|≤x<2}D.{x|<x<2}8.函数f(x)=x2﹣4x+5在区间[0,m]上的最大值为5,最小值为1,则m的取值范围是()A.[2,+∞)B.[2,4]C.(﹣∞,2]D.[0,2]19.(5分)(2016淄博一模)三棱锥S﹣ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为()A.2B.4C.D.1610.(5分)(2015秋蒙城县校级期末)使得函数f(x)=lnx+x﹣2有零点的一个区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)11.(5分)(2015株洲一模)如图,在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为()A.B.C.D.12.(5分)(2015秋广西期末)已知y=loga(2﹣ax)是[0,1]上的减函数,则a的取值范围为()A.(0,1)B.(1,2)C.(0,2)D.[2,+∞)二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)(2015秋蒙城县校级期末)函数的定义域是.214.与直线2x+y+1=0的距离为的直线方程为.15.如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是.16.设函数f(x)=ax+bx﹣cx,其中c>a>0,c>b>0.若a,b,c是△ABC的三条边长,则下列结论正确的是.①对任意x∈(﹣∞,1),都有f(x)<0;②存在x∈R,使ax,bx,cx不能构成一个三角形的三条边长;③若△ABC为钝角三角形,存在x∈(1,2)使f(x)=0.三、解答题:本大题共70分,解答应写出文字说明,证明过程或演算步骤.17.(10分)(2015秋邵阳校级期末)设圆上的点A(2,﹣3)关于直线x+2y=0的对称点仍在这个圆上,且圆与y轴相切,求圆的方程.18.(12分)(2013江苏)如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.19.(12分)(2015秋太和县期末)设A={x|x≥1或x≤﹣3},B={x|﹣4<x<0}求:(2)A∩B,A∪B(2)A∪(∁RB)20.(12分)(2015秋邵阳校级期末)已知函数f(x)=logax(a>0,a≠1),且f(3)﹣f(2)=1.(1)若f(3m﹣2)<f(2m+5),求实数m的取值范围.(2)求使f(x﹣)=成立的x的值.321.(12分)(2009秋锦州期末)已知函数是奇函数,且.(Ⅰ)求函数f(x)的解析式;(Ⅱ)用定义证明函数f(x)在(0,1)上的单调性.22.(12分)(2015秋邵阳校级期末)已知O为坐标原点,△AOB中,边OA所在的直线方程是y=3x,边AB所在的直线方程是y=﹣,且顶点B的横坐标为6.(1)求△AOB中,与边AB平行的中位线所在直线的方程;(2)求△AOB的面积;(3)已知OB上有点D,满足△AOD与△ABD的面积比为2,求AD所在的直线方程.2015-2016学年湖南省邵阳市洞口一中高一(上)期末数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,在每小题列出的四个选项中,只有一项是符合题目要求的.1.函数y=ax+2(a>0且a≠1)图象一定过点()A.C.【考点】指数函数的单调性与特殊点.【专题】函数的性质及应用.【分析】由于函数y=ax(a>0且a≠1)图象一定过点(0,1),可得...