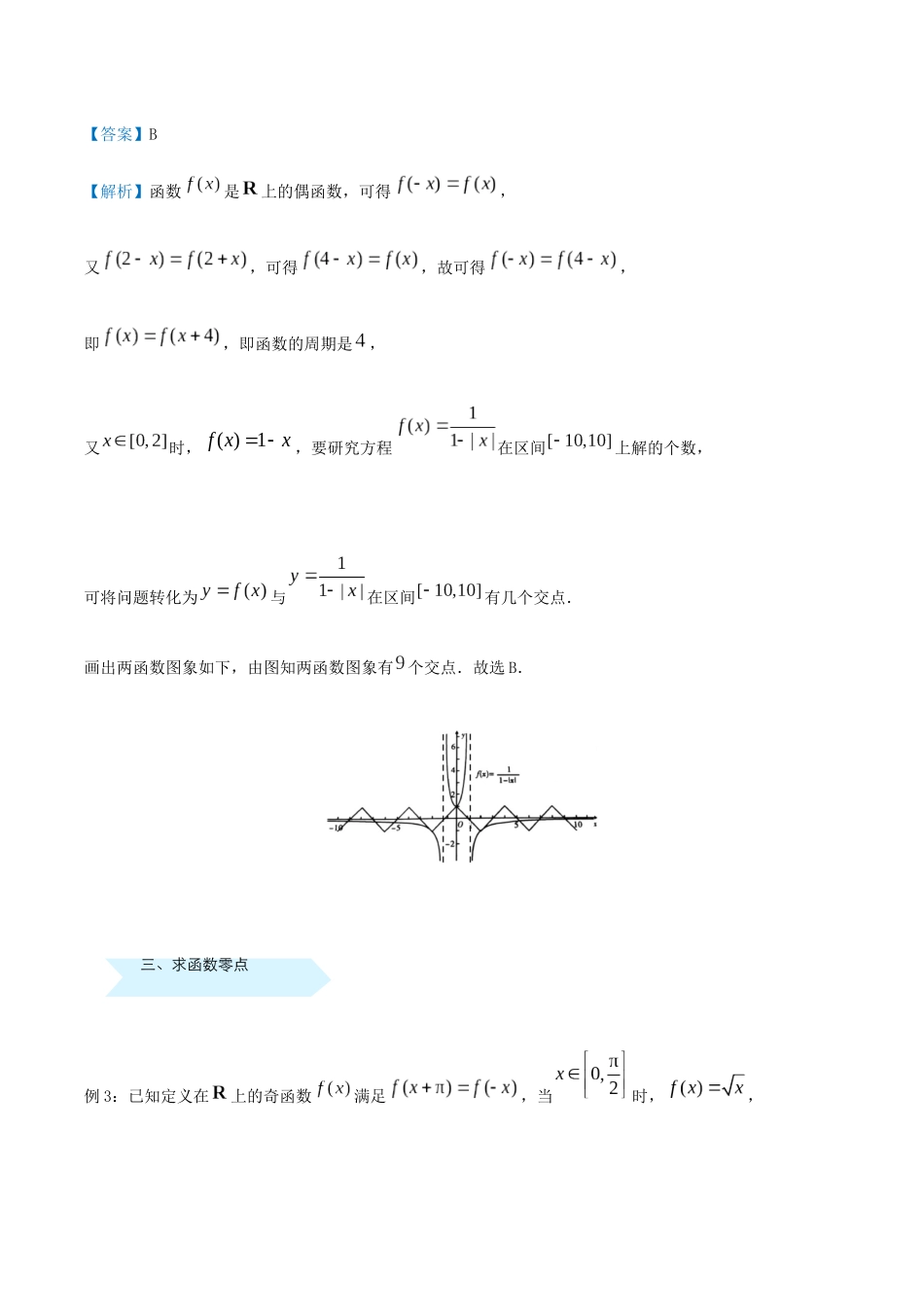
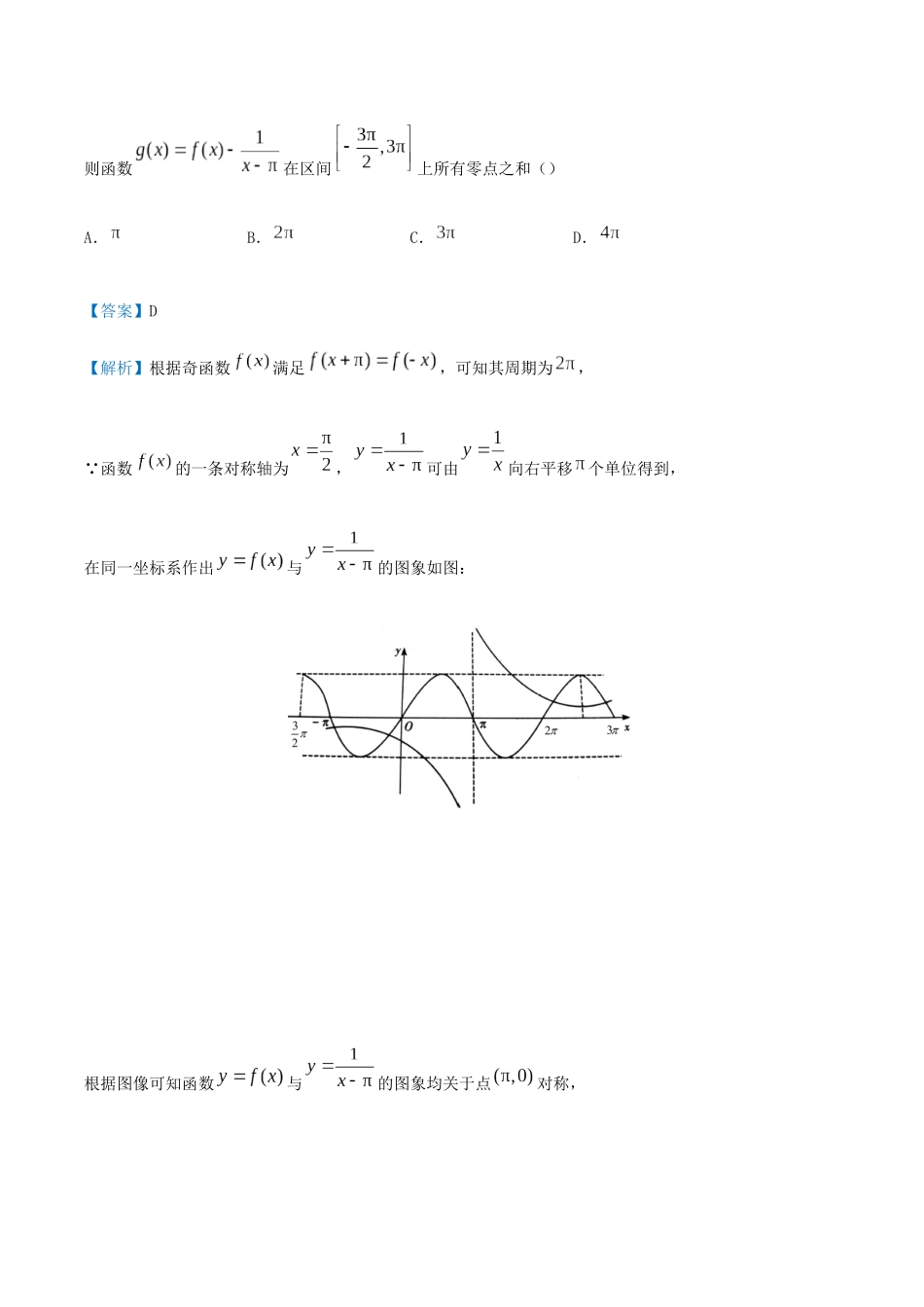
一、运用零点存在性定理判断函数零点所在区间二、函数零点个数的判定培优点二函数零点例1:函数的零点所在的区间为()A.B.C.D.【答案】B【解析】由题意可知原函数是上的增函数,,,故根据零点存在定理得到零点存在于上,故选B.例2:已知函数是偶函数,且,当时,,则方程在区间上解的个数是()A.B.C.D.三、求函数零点【答案】B【解析】函数是上的偶函数,可得,又,可得,故可得,即,即函数的周期是,又时,,要研究方程在区间上解的个数,可将问题转化为与在区间有几个交点.画出两函数图象如下,由图知两函数图象有个交点.故选B.例3:已知定义在上的奇函数满足,当时,,则函数在区间上所有零点之和()A.B.C.D.【答案】D【解析】根据奇函数满足,可知其周期为, 函数的一条对称轴为,可由向右平移个单位得到,在同一坐标系作出与的图象如图:根据图像可知函数与的图象均关于点对称,四、根据函数零点情况求参数的取值范围且函数与的图象在区间上有四个交点,所以函数在区间上所有零点之和为,故选D.例4:函数,方程有个不相等实根,则的取值范围是()A.B.C.D.【答案】C【解析】根据题意画出函数的图象:设,有两个不同的根,,五、二分法故当时,将代入方程得到,此时关于的方程的根是,,故不符合题意;当时,当时,关于的方程有唯一实数解,当时,关于的方程有三个实数解,故方程有个不相等实根,符合题意要求,所以,故答案为C.例5:在用二分法求函数在区间上的唯一零点的过程中,取区间上的中点,若,则函数在区间上的唯一零点()对点增分集训A.在区间内B.在区间内C.在区间或内D.等于【答案】D【解析】根据用二分法求方程的近似解的方程和步骤,函数在区间上的唯一零点.故选D.一、选择题1.函数的零点一定位于区间()A.B.C.D.【答案】B【解析】易知函数在其定义域上是增函数,因为,,所以函数的零点一定位于区间内.故选B.2.函数的零点所在的区间是()A.B.C.D.【答案】B【解析】因为,,.所以函数零点所在的区间是,故选B.3.函数在上的所有零点之和等于()A.B.C.D.【答案】D【解析】由,得,分别作出函数与的图象,由图象可知函数的对称性,可知两函数图象均关于对称.由图可知,函数在上的所有零点之和等于.故选D.4.已知是定义在上且以为周期的奇函数,当时,,则函数在区间上的零点个数是()A.B.C.D.【答案】D【解析】因为函数为奇函数,所以在上必有.当时,由,得,即,解得.因为函数是周期为的奇函数,所以,此时在区间上有个零点,,.,此时在区间上有四个零点,,,.当时,,所以,即,此时在区间上有两个零点,.所以共有个零点.故选D.5.用二分法求如图所示函数的零点时,不可能求出的零点是()A.B.C.D.【答案】C【解析】二分法求函数的零点时,函数必须满足在零点两侧的函数值异号,而图中函数在零点的两侧的函数值都是负值,故不能用二分法求出.故选C.6.定义域为的偶函数满足对,有,且当时,,若函数至少有个零点,则的取值范围是()A.B.C.D.【答案】B【解析】令,,∴,∴图象关于直线对称,画出函数与函数的图象如下,由图可知,要使至少要有个零点,即函数与的图像至少要有个交点,则有,且点在函数的下方,即,故选B.7.已知是函数在上的所有零点之和,则的值为()A.B.C.D.【答案】B【解析】函数在上的所有零点之和,即在上的所有实数根之和,即在上的所有实数根之和.令,,因为可知函数的图象关于直线对称,函数的图象也关于直线对称,作出两个函数的大致图象,如图所示,由图象知,两个函数的图象有个交点,且个交点的横坐标之和为,故选B.8.已知函数,关于的方程有个不同的实数解,则的取值范围是()A.B.C.D.【答案】C【解析】设,则,由,解得,当时,,函数为增函数;时,,函数为减函数,当时,函数取得极大值也是最大值为.方程化为,解得或.画出函数的图象如图:根据图象可知的取值范围是时,方程有个解.故选C.9.已知定义域为的偶函数满足对任意的,有,且当时,.若函数在上恰有三个零点,则实数的取值范围是()A.B.C.D.【答案】B【解...