D2_1导数概念VIP免费

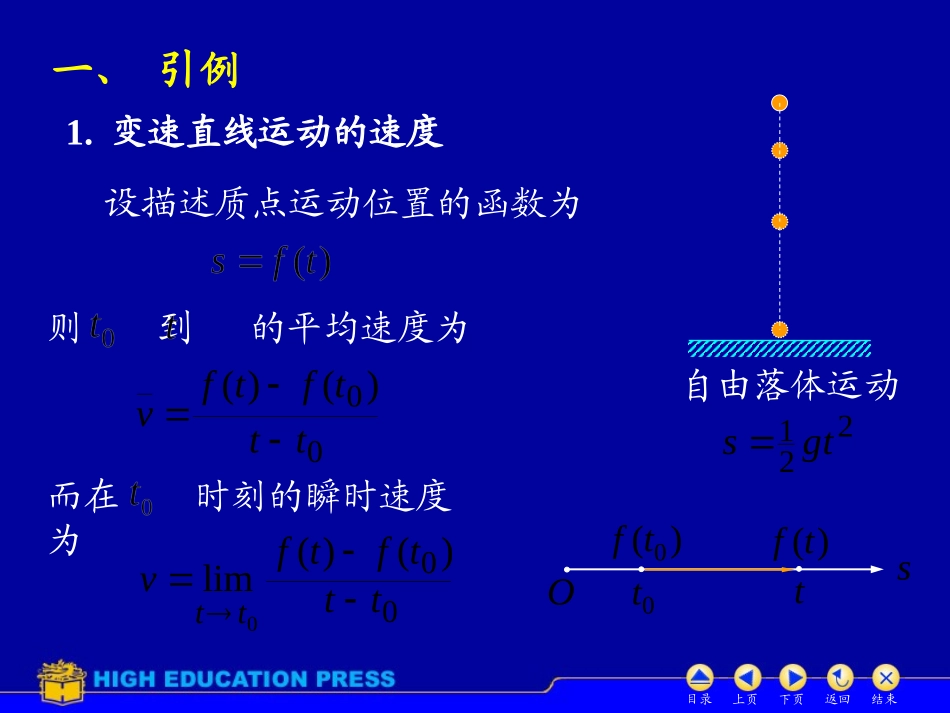
第二章微积分学的创始人:德国数学家Leibniz微分学导数描述函数变化快慢微分描述函数变化程度都是描述物质运动的工具(从微观上研究函数)导数与微分导数思想最早由法国数学家Ferma在研究极值问题中提出.英国数学家Newton目录上页下页返回结束一、引例二、导数的定义三、导数的几何意义四、函数的可导性与连续性的关系五、单侧导数第一节导数的概念第二章目录上页下页返回结束sO一、引例1.变速直线运动的速度设描述质点运动位置的函数为则到的平均速度为v)()(0tftf0tt而在时刻的瞬时速度为lim0ttv)()(0tftf0tt221tgs自由落体运动0t)(0tf)(tft目录上页下页返回结束2.曲线的切线斜率曲线NT0xM在M点处的切线x割线MN的极限位置MT(当时)割线MN的斜率tan)()(0xfxf0xx切线MT的斜率tanlimlim0xxk)()(0xfxf0xxxy)(xfyCO目录上页下页返回结束两个问题的共性:瞬时速度切线斜率所求量为函数增量与自变量增量之比的极限.类似问题还有:加速度角速度线密度电流强度是速度增量与时间增量之比的极限是转角增量与时间增量之比的极限是质量增量与长度增量之比的极限是电量增量与时间增量之比的极限变化率问题NT0xMxxy)(xfyCOsO0t)(0tf)(tft目录上页下页返回结束二、导数的定义定义1.设函数在点0limxx00)()(xxxfxfxyx0lim)()(0xfxfy0xxx存在,并称此极限为记作:;0xxy;)(0xf;dd0xxxy0d)(dxxxxf即0xxy)(0xfxyx0lim则称函数若的某邻域内有定义,在点处可导,在点的导数.目录上页下页返回结束运动质点的位置函数)(tfs在时刻的瞬时速度0t曲线)(:xfyC在M点处的切线斜率)(0tf)(0xfsO0t)(0tf)(tftNT0xMxxy)(xfyCO目录上页下页返回结束)()(0xfxfy0xxx不存在,就说函数在点不可导.0x若0lim,ΔΔΔxyx也称在若函数在开区间I内每点都可导,此时导数值构成的新函数称为导函数.记作:;y;)(xf;ddxy.d)(dxxf注意:)(0xf0)(xxxfxxfd)(d0就称函数在I内可导.的导数为无穷大.若极限目录上页下页返回结束例1.求函数(C为常数)的导数.解:y即例2.求函数解:axafxf)()(axlimaxaxnnaxlim(limax1nx2nxa32nxa)1naxxfxxf)()(0limx目录上页下页返回结束说明：对一般幂函数xy(为常数)1)(xx例如，)(x)(21x2121xx21x1)(1x11x21x)1(xx)(43x4743x（以后将证明）目录上页下页返回结束hxhxhsin)sin(lim0例3.求函数的导数.解:则hxfhxf)()(0limh0limh)2cos(2hx)2cos(lim0hxhxcos即xxcos)(sin类似可证得xxsin)(cos目录上页下页返回结束例4.求函数的导数.解:hxfhxf)()(0limhhxhxhln)ln(lim0hh1lim0即xx1)(ln0limhh1x1x0limheln目录上页下页返回结束则令,0hxt原式是否可按下述方法作:例5.证明函数在x=0不可导.证:hfhf)0()0(hh0h,10h,1hfhfh)0()0(lim0不存在,例6.设存在,求极限.2)()(lim000hhxfhxfh解:原式0limh)(0xfhhxf2)(0)(0xf)(210xf)(210xf)(0xf)(2)(0hhxf)(0xf目录上页下页返回结束三、导数的几何意义曲线在点的切线斜率为)(tan0xf若曲线过上升;若曲线过下降;xyO0x),(00yx若切线与x轴平行,称为驻点;若切线与x轴垂直.曲线在点处的切线方程:法线方程:)0)((0xfxyO)(xfyCT0xMxy0xO目录上页下页返回结束xyO1111例7.问曲线哪一点有铅直切线?哪一点处的切线与直线平行?写出其切线方程.解:3231x,0xy令,3113132x得,1x对应,1y则在点(1,1),(–1,–1)处与直线平行的切线方程分别为即故在原点(0,0)有铅直切线目录上页下页返回结束四、函数的可导性与连续性的关系定理1.证:设在点x处可导,存在,因此必有其中故0x所以函数在点x连续.注意:函数在点x连续，但在该点未必可导.反例:xy在x=0处连续,但不可导.即xyO目录上页下页返回结束在点的某个右邻域...