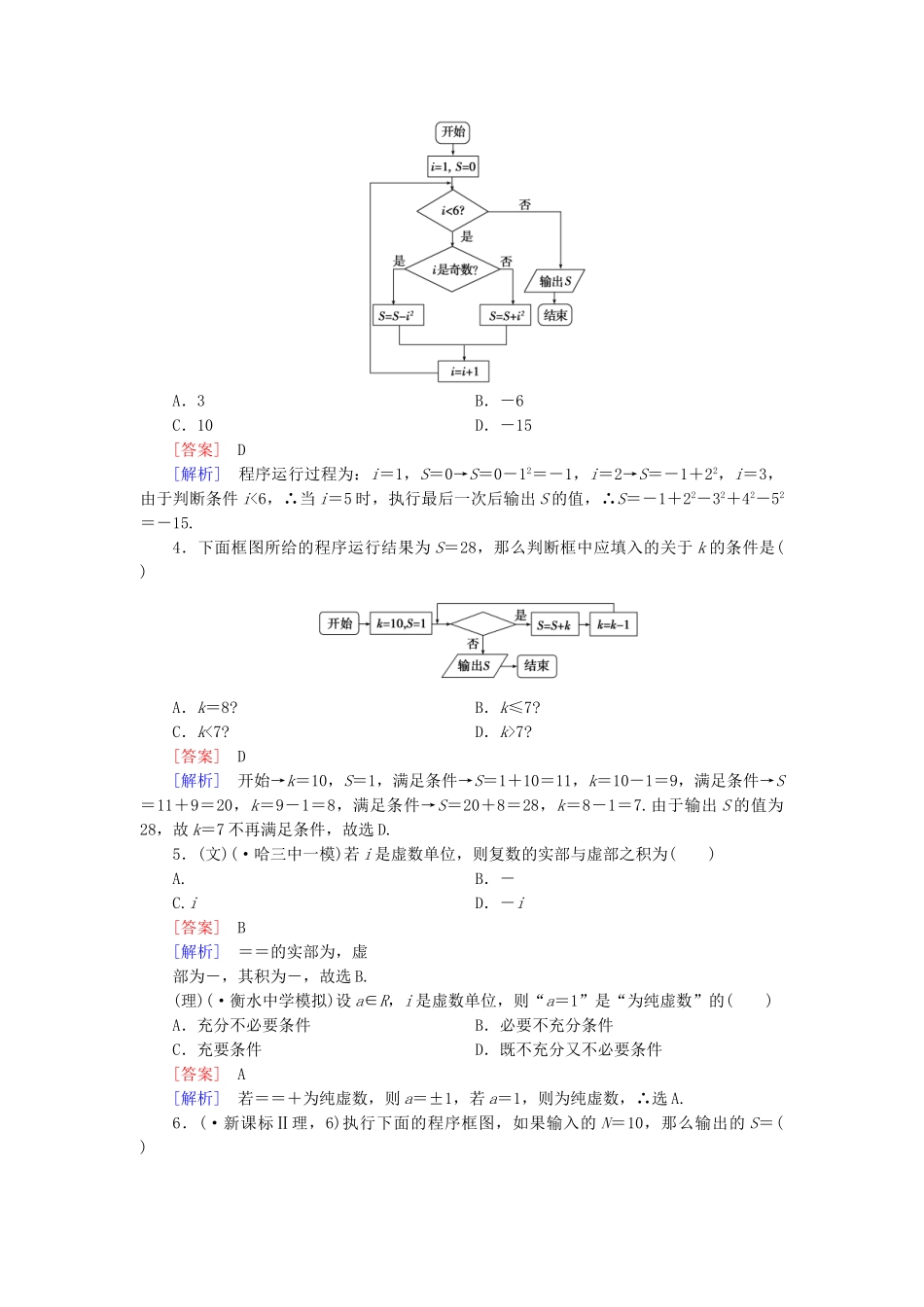
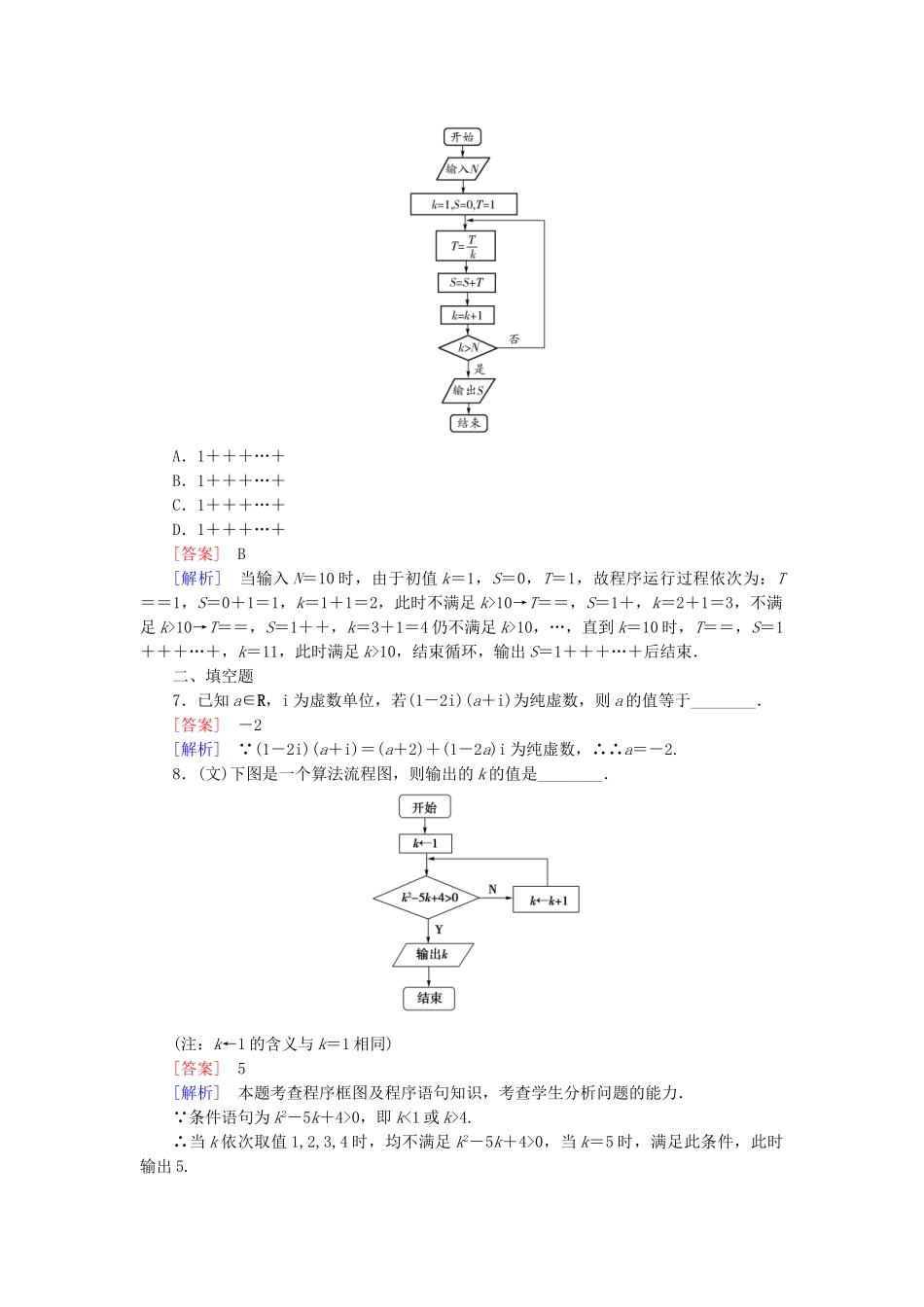
【成才之路】届高考数学二轮复习专题6第3讲算法框图与复数素能训练(文、理)一、选择题1.(·浙江理,2)已知i是虚数单位,a,b∈R,则“a=b=1”是“(a+bi)2=2i”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件[答案]A[解析]本题考查充分条件、必要条件及复数的运算,当a=b=1时,(a+bi)2=(1+i)2=2i,反之,(a+bi)2=a2-b2+2abi=2i,则a2-b2=0,2ab=1,解a=1,b=1或a=-1,b=-1,故a=1,b=1是(a+bi)2=2i的充分不必要条件,选A.2.(文)(·广东文,3)若i(x+yi)=3+4i,x、y∈R,则复数x+yi的模是()A.2B.3C.4D.5[答案]D[解析]由i(x+yi)=xi+yi2=-y+xi=3+4i,知x=4,y=-3,则x+yi的模为=5.(理)(·甘肃三诊)若(1+2ai)i=1-bi,其中a、b∈R,则|a+bi|=()A.+iB.C.D.[答案]C[解析] (1+2ai)i=-2a+i=1-bi,∴a=-,b=-1,∴|a+bi|=|--i|==.3.(文)(·东北三省三校一模)执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=,④f(x)=x2,则输出的函数是()A.f(x)=sinxB.f(x)=cosxC.f(x)=D.f(x)=x2[答案]A[解析] 函数f(x)=sinx是奇函数且存在零点,∴输出的函数是f(x)=sinx.(理)(·山西省重点中学四校联考)执行如图所示的程序框图,则输出S的值为()A.3B.-6C.10D.-15[答案]D[解析]程序运行过程为:i=1,S=0→S=0-12=-1,i=2→S=-1+22,i=3,由于判断条件i<6,∴当i=5时,执行最后一次后输出S的值,∴S=-1+22-32+42-52=-15.4.下面框图所给的程序运行结果为S=28,那么判断框中应填入的关于k的条件是()A.k=8?B.k≤7?C.k<7?D.k>7?[答案]D[解析]开始→k=10,S=1,满足条件→S=1+10=11,k=10-1=9,满足条件→S=11+9=20,k=9-1=8,满足条件→S=20+8=28,k=8-1=7.由于输出S的值为28,故k=7不再满足条件,故选D.5.(文)(·哈三中一模)若i是虚数单位,则复数的实部与虚部之积为()A.B.-C.iD.-i[答案]B[解析]==的实部为,虚部为-,其积为-,故选B.(理)(·衡水中学模拟)设a∈R,i是虚数单位,则“a=1”是“为纯虚数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件[答案]A[解析]若==+为纯虚数,则a=±1,若a=1,则为纯虚数,∴选A.6.(·新课标Ⅱ理,6)执行下面的程序框图,如果输入的N=10,那么输出的S=()A.1+++…+B.1+++…+C.1+++…+D.1+++…+[答案]B[解析]当输入N=10时,由于初值k=1,S=0,T=1,故程序运行过程依次为:T==1,S=0+1=1,k=1+1=2,此时不满足k>10→T==,S=1+,k=2+1=3,不满足k>10→T==,S=1++,k=3+1=4仍不满足k>10,…,直到k=10时,T==,S=1+++…+,k=11,此时满足k>10,结束循环,输出S=1+++…+后结束.二、填空题7.已知a∈R,i为虚数单位,若(1-2i)(a+i)为纯虚数,则a的值等于________.[答案]-2[解析] (1-2i)(a+i)=(a+2)+(1-2a)i为纯虚数,∴∴a=-2.8.(文)下图是一个算法流程图,则输出的k的值是________.(注:k←1的含义与k=1相同)[答案]5[解析]本题考查程序框图及程序语句知识,考查学生分析问题的能力. 条件语句为k2-5k+4>0,即k<1或k>4.∴当k依次取值1,2,3,4时,均不满足k2-5k+4>0,当k=5时,满足此条件,此时输出5.[点评]将程序框图与一元二次不等式结合是一种新颖命题方式,注意从中得到的备考启示.(理)如图所示,程序框图(算法流程图)的输出结果是________.[答案]15[解析]由T=T+k可知T是一个累加变量,原题实质为求1+2+3+…+k的和,其和为.令≤105,得k≤14.故当k=15时,T=1+2+3+…+5=120>105,此时输出k=15.9.(·江苏四市调研)若复数z满足z-2=i(1+i)(i为虚数单位),则z=________.[答案]1-i[解析]设z=a+bi(a,b∈R),∴a-bi-2=i-1,∴∴∴z=1-i.10.设复数z在复平面上对应点为A(1,-3),AB=(-2,5),点B对应的复数为z1,则|z1|=________.[答案][解析] OB=OA+AB=(1,-3)+(-2,5)=(-1,2),∴z1=...