《学案与测评》2011年高考数学总复习 第三单元第一节 二次函数精品课件 苏教版VIP免费

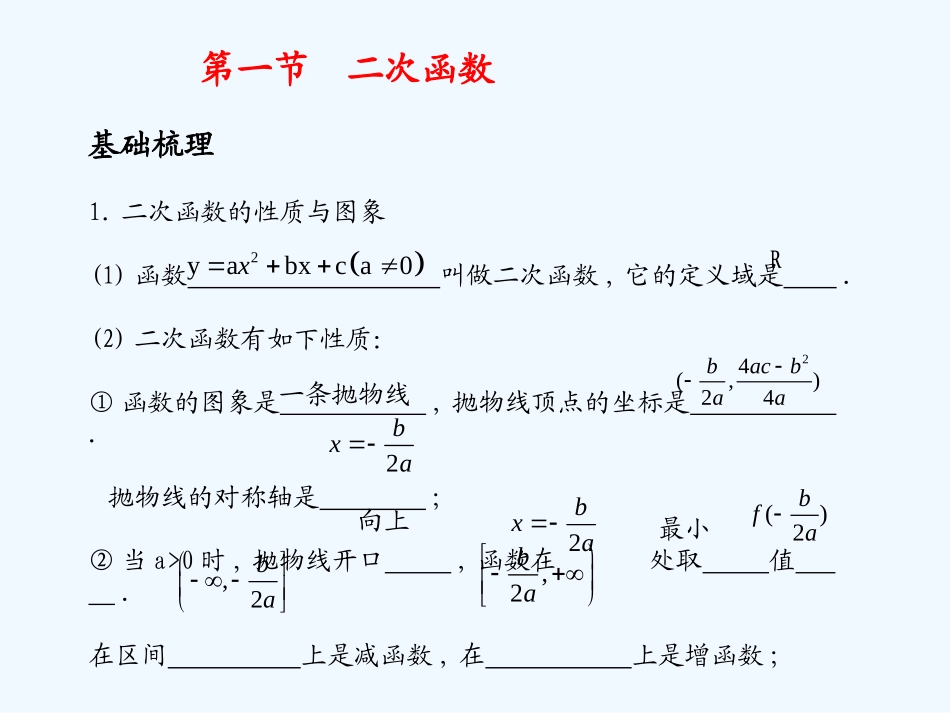
第一节二次函数基础梳理一条抛物线向上最小2yabxca0xR2bxa24(,)24bacbaa1.二次函数的性质与图象(1)函数叫做二次函数,它的定义域是.(2)二次函数有如下性质：①函数的图象是,抛物线顶点的坐标是.抛物线的对称轴是;②当a>0时,抛物线开口,函数在处取值.在区间上是减函数,在上是增函数;2bxa()2bfa,2ba,2ba③当a<0时,抛物线开口,函数在处取值在区间上是增函数,在上是减函数向下最大()2bfa2bxa,2ba,2ba(0,c)④与y轴的交点是;⑤当Δ=-4ac>0时,与x轴两交点的横坐标分别是方程的两根;当Δ=0时,与x轴切于一点;当Δ<0时,与x轴;⑥当b≠0时,是非奇非偶函数;当b=0时,是;2b12,xx没有交点2axbxc0a0偶函数(,0)2ba⑦对于函数f(x),若对任意自变量x的值,都有f(a+x)=f(a-x),则f(x)的图象关于直线对称.x=a2.二次函数、一元二次方程、一元二次不等式三者之间的关系判别式Δ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象一元二次方程的根有两相异实根x1,x2(x10(a>0)的解集...ax2+bx+c<0(a>0)的解集...{x|x∈R}12x|xxxx或1x|xx12x|xxxmaxfm,fn(2)h∈[m,n]时,当hn时,f(x)在[m,n]上单调,..minymaxyf(n)f(m)题型一二次函数图象和性质的应用【例1】已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定此二次函数的解析式.分析由题目条件知二次函数过(2,-1),(-1,-1)两点,且知其最大值,所以可应用一般式、顶点式或两根式解题.解方法一:利用二次函数一般式.设f(x)=2axbxca0由题意得24a2bc-1,a-4,a-bc-1,b4,c7,4ac-b8,4a解得∴所求二次函数为2y4x4x7方法二:利用二次函数顶点式.设f(x)=a(x-m)2+n(a≠0). f(2)=f(-1),∴抛物线对称轴为∴又根据题意,函数有最大值f(x)max=8,212(-1)2x21m22221f(x)a(x-)8.21f(2)-1,a(2-)8-1a-4.21f(x)-4(x-)8-4x4x7.2解得方法三:利用两根式.由已知f(x)+1=0的两根为,故可设f(x)+1=a(x-2)(x+1)(a≠0),即.又函数有最大值f(x)max=8,即解得a=-4，或a=0(舍去).故所求函数解析式为.12x2,x12fxaxax2a12fx4x4x7学后反思求二次函数的解析式的关键是求待定系数的值.由题目的条件,合理地选择二次函数解析式的表达形式,最简单地求出解析式是关键.举一反三1.右图是一个二次函数的图像（1）写出这个二次函数的零点；（2）求这个二次函数的解析式；（3）当实数k在和范围内变化时，g(x)=f(x)-kx在区间上是单调函数22，解析：（1）由图可知二次函数的零点为-3，1.（2）设二次函数为y=a(x+3)(x-1)，由点（-1，4）在函数上，得a=-1，则y=-(x+3)(x-1)=223xx(3)g(x)=开口向下，对称轴为当，即k≥2时，g(x)在上单调递减当,即k≤-6时，g(x)在上单调递增综上所述，当k≤-6或k≥2时，g(x)在区间上是单调函数2223(2)3,xxkxxkx22kx222k2,2222k2,22,2题型二轴定区间动【例2】已知，若f(x)的最小值为h(t)，写出h(t)的表达式2()35,,1fxxxxtt分析在对称轴确定的情况下，对区间进行分析,1tt解二次函数的图像的对称轴(1)当（2）当32x2351,()(1)5122tthtfttt即353222t