《321几类不同增长的函数模型(2)》课件VIP免费

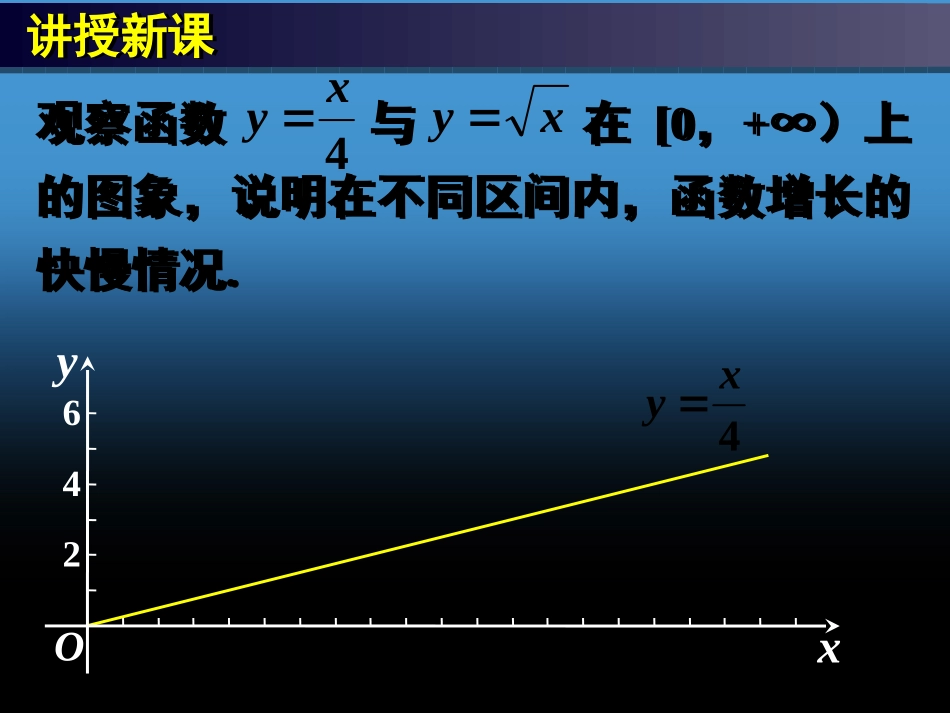
讲授新课讲授新课642xyO观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.4xyxy讲授新课讲授新课642xy4xyO观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.4xyxy讲授新课讲授新课642xy4xyxyO观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.4xyxy讲授新课讲授新课64216xy4xyxyO观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.观察函数与在[0，+∞）上的图象，说明在不同区间内，函数增长的快慢情况.4xyxy实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.8642-22468xyO实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.8642-22468xyOxy2实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.8642-22468xyOxy22xy实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.8642-22468xyOxy22xyxy2log实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.实例探究：比较函数y=2x，y=x2，y=log2x的增长快慢.8642-22468xyO你能分别求出使222logxxxxxx2log22成立的x的取值范围吗？xy22xyxy2log放大后的图象放大后的图象30282624222018161412108642510xyOxy22xy规律总结规律总结①一般地，对于指数函数y=ax(a＞1)和幂函数y=xn(n＞0)，在区间[0，+∞)上，无论n比a大多少，尽管在x的一定变化范围内，ax会小于xn，但由于ax的增长快于xn的增长，因此总存在一个x0，当x＞x0时，就会有ax＞xn.①一般地，对于指数函数y=ax(a＞1)和幂函数y=xn(n＞0)，在区间[0，+∞)上，无论n比a大多少，尽管在x的一定变化范围内，ax会小于xn，但由于ax的增长快于xn的增长，因此总存在一个x0，当x＞x0时，就会有ax＞xn.规律总结规律总结②对于对数函数y=logax(a＞1)和幂函数y=xn(n＞0)在区间[0，+∞)上，随着x的增大，logax增长得越来越慢.在x的一定变化范围内，logax可能会大于xn，但由于logax的增长慢于xn的增长，因此总存在一个x0，当x＞x0时，就会有logax＜xn.②对于对数函数y=logax(a＞1)和幂函数y=xn(n＞0)在区间[0，+∞)上，随着x的增大，logax增长得越来越慢.在x的一定变化范围内，logax可能会大于xn，但由于logax的增长慢于xn的增长，因此总存在一个x0，当x＞x0时，就会有logax＜xn.规律总结规律总结③在区间[0，+∞)上，尽管函数y=ax(a＞1)，y=logax(a＞1)和y=xn(n＞0)都是增函数，但它们的增长速度不同，而且不在同一个“档次”上.随着x的增长，y=ax(a＞1)的增长速度越来越快，会超过并远远大于y=xn(n＞0)的增长速度，而y=logax(a＞1)的增长速度则会越来越慢.因此，总会存在一个x0，当x＞x0时，就有logax＜xn＜ax.③在区间[0，+∞)上，尽管函数y=ax(a＞1)，y=logax(a＞1)和y=xn(n＞0)都是增函数，但它们的增长速度不同，而且不在同一个“档次”上.随着x的增长，y=ax(a＞1)的增长速度越来越快，会超过并远远大于y=xn(n＞0)的增长速度，而y=logax(a＞1)的增长速度则会越来越慢.因此，总会存在一个x0，当x＞x0时，就有logax＜xn＜ax.举例分析举例分析例1同一坐标系中，函数y=x2+7和y=2x的图象如图.试比较x2+7与2x的大小.例1同一坐标系中，函数y=x2+7和y=2x的图象如图.试比较x2+7与2x的大小.5040302010510y＝x2＋7y＝2xxyO举例分析举例分析例2已知函数y=x2和y=log2(x+1)的图象如图，试比较x2与log2(x+1)的大小.例2已知函数y=x2和y=log2(x+1)的图象如图，试比较x2与log2(x+1)的大小.4321-124xyOy＝x2y＝log2(x＋1)-1课堂小结：课堂小结：1．幂函数、指数函数、对函数增长快慢的差异；2．体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义.1．幂函数、指数函数、对函数增长快慢的差异；2．体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义.课后作业：课后作业：1.预习教材2.《习案》作业三十二.1.预习教材2.《习案》作业三十二.