D3_3泰勒公式VIP免费

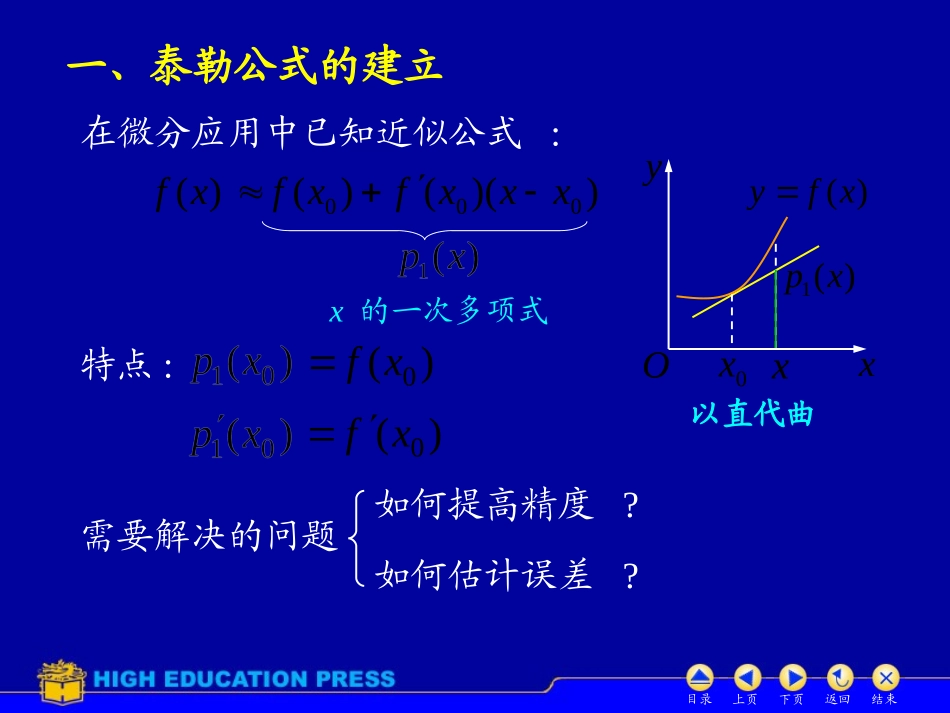
目录上页下页返回结束二、几个初等函数的麦克劳林公式第三节一、泰勒公式的建立三、泰勒公式的应用应用目的－用多项式近似表示函数.理论分析近似计算泰勒公式第三章目录上页下页返回结束特点:)(0xf)(0xf一、泰勒公式的建立)(xf))(()(000xxxfxf以直代曲0x)(1xp在微分应用中已知近似公式:需要解决的问题如何提高精度?如何估计误差?xx的一次多项式xy)(xfyO目录上页下页返回结束1.求n次近似多项式要求:)(0!212xpan,)(0xf,)(0)(!1xpannnn)(0)(xfn故)(xpn)(0xf))((00xxxf!21!1nnnxxxf))((00)(!1n200))((xxxf!21令)(xpn则)(xpn)(xpnnan!)()(xpnn)(00xpan,)(0xf)(01xpan,)(0xf1a)(202xxa10)(nnxxan2!2a20)()1(nnxxann0annxxaxxaxxa)()()(020201目录上页下页返回结束)0(之间与在nx)()(10nnxxxR)(2)1()(0)(xnRnnnn2.余项估计)()()(xpxfxRnn令(称为余项),)(0xRn)(0xRn0)(0)(xRnn10)()(nnxxxRnnxnR))(1()(011))(1()(011nnxnR1022)()1()(nnxnnR!)1()()1(nRnn则有)(0xRn0)(0xRn0)(0)(xRnn0x)01(之间与在xx)102(之间与在x目录上页下页返回结束)()()(xpxfxRnn)0(之间与在xx,0)()1(xpnn10)1()(!)1()()(nnnxxnfxR)()()1()1(xfxRnnn时的某邻域内当在Mxfxn)()1(0)0(之间与在xx10!)1()(nnxxnMxR)())(()(00xxxxoxRnn目录上页下页返回结束公式①称为的n阶泰勒公式.公式②称为n阶泰勒公式的拉格朗日余项.泰勒(Taylor)中值定理:阶的导数,时,有)(0xf))((00xxxf200)(!2)(xxxfnnxxnxf)(!)(00)()(xRn①其中10)1()(!)1()()(nnnxxnfxR②则当)0(之间与在xx泰勒目录上页下页返回结束公式③称为n阶泰勒公式的佩亚诺(Peano)余项.在不需要余项的精确表达式时,泰勒公式可写为)(0xf))((00xxxf200)(!2)(xxxfnnxxnxf)(!)(00)(])[(0nxxo])[()(0nnxxoxR注意到③④*可以证明:④式成立目录上页下页返回结束特例:(1)当n=0时,泰勒公式变为)(xf)(0xf))((0xxf(2)当n=1时,泰勒公式变为给出拉格朗日中值定理)(xf)(0xf))((00xxxf20)(!2)(xxf可见误差)(xf)(0xf))((00xxxf10)1()(!)1()(nnxxnf200)(!2)(xxxfnnxxnxf)(!)(00)(fd)0(之间与在xx)0(之间与在xx)0(之间与在xx)0(之间与在xx目录上页下页返回结束称为麦克劳林(Maclaurin)公式.,00x则有)0(fxf)0(2!2)0(xfnnxnf!)0()(在泰勒公式中若取)(xf)(0xf))((00xxxf10)1()(!)1()(nnxxnf200)(!2)(xxxfnnxxnxf)(!)(00)()0(之间与在xx)(xf)0(fxf)0(,)()1(Mxfn则有误差估计式1!)1()(nnxnMxR2!2)0(xfnnxnf!)0()(若在公式成立的区间上麦克劳林由此得近似公式,)10(x记目录上页下页返回结束二、几个初等函数的麦克劳林公式,e)()(xkxf),2,1(1)0()(kfkxe1x!33x!nxn)(xRn!22x其中)0(fxf)0(2!2)0(xfnnxnf!)0()(麦克劳林公式)10(目录上页下页返回结束π)sin(212mx)cos()1(xm)sin(x)()(xfkxsinx!33x!55x!)12(12mxm)(2xRm其中)(2xRm2πk2πsin)0()(kfkmk2,012mk,)1(1m),2,1(m1)1(m)10(12mx!)12(m)0(fxf)0(2!2)0(xfnnxnf!)0()()10(麦克劳林公式目录上页下页返回结束麦克劳林公式!)2(2mxm类似可得xcos1!22x!44x)(12xRm其中)(12xRm!)22(m)cos()1(1xm)10(m)1(22mx)0(fxf)0(2!2)0(xfnnxnf!)0()()10(目录上页下页返回结束)()(xfk)1(x1x2xnx)(xRn其中)(xRn11)1(!)1()()1(nnxxnn...