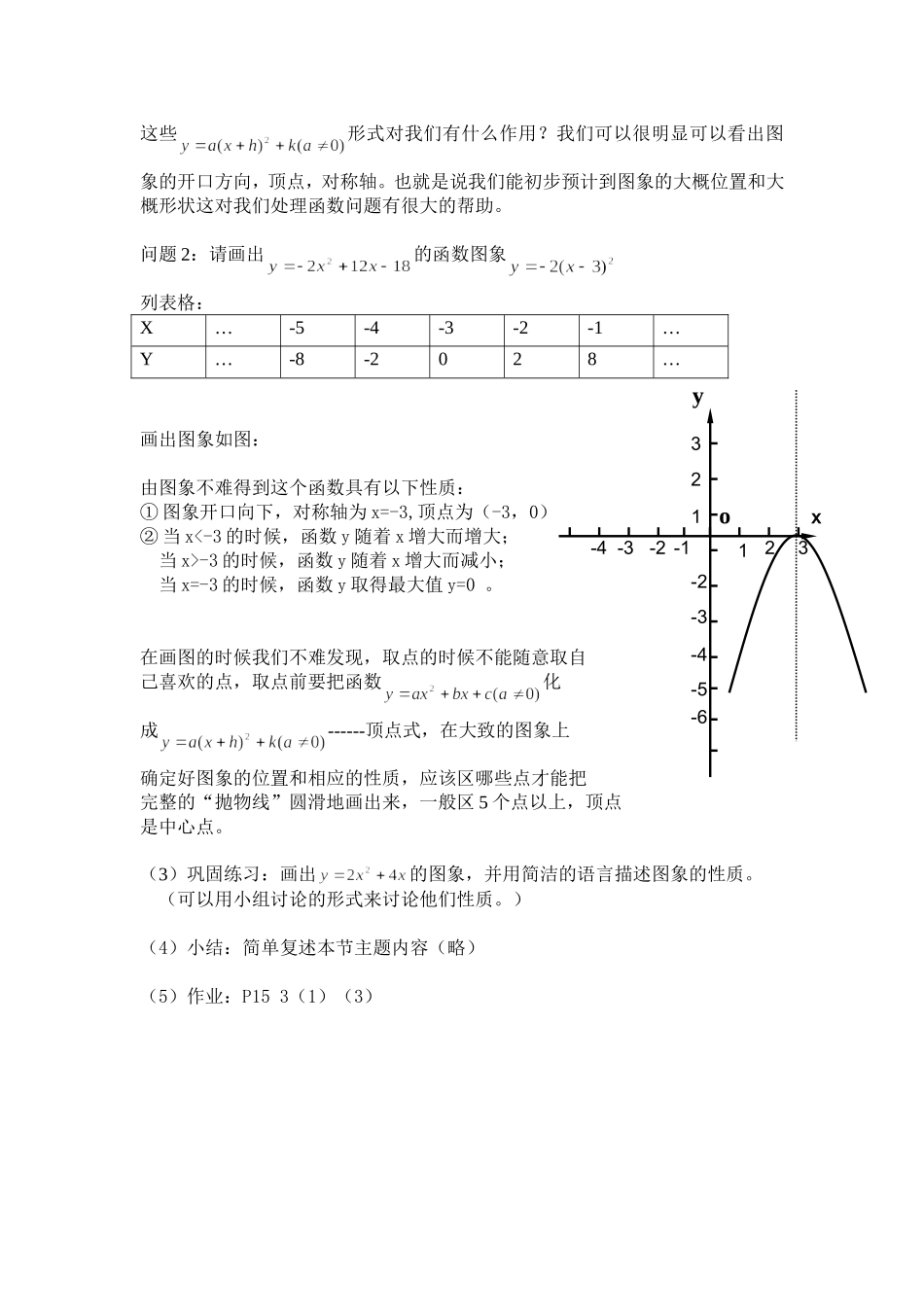
二次函数图象和性质(3)(教学设计)一.教学目标:①掌握二次函数平移三种形式;②理解并能运用二次函数平移三种形式初步确立二次函数相关要素;③能对二次函数配方,并研究其图象;④培养学生的观察能力和逻辑推理能力,严格要求学生对数学语言的正确表述。二.重点难点:重点:配方法研究二次函数图象和性质。难点:画出二次函数图象。三.教学设计:(1)复习(投影):①根据函数的图象求:(1)x=1时,y的值;(2)y=1时,x的值。②填表格开口方向对称轴顶点坐标总结归纳规律:投影、、三者关系。(2)新授:问题1:我们研究了的形式是经过了的图象经历了一系列的平移的得到的,但是我们遇到的二次函数的形式往往是,我们应该如何把两者联系在一起的?用什么方法联系?(配方法)用配方法把下面的式子变成形式。①②③④这些形式对我们有什么作用?我们可以很明显可以看出图象的开口方向,顶点,对称轴。也就是说我们能初步预计到图象的大概位置和大概形状这对我们处理函数问题有很大的帮助。问题2:请画出的函数图象列表格:X…-5-4-3-2-1…Y…-8-2028…画出图象如图:由图象不难得到这个函数具有以下性质:①图象开口向下,对称轴为x=-3,顶点为(-3,0)②当x<-3的时候,函数y随着x增大而增大;当x>-3的时候,函数y随着x增大而减小;当x=-3的时候,函数y取得最大值y=0。在画图的时候我们不难发现,取点的时候不能随意取自己喜欢的点,取点前要把函数化成------顶点式,在大致的图象上确定好图象的位置和相应的性质,应该区哪些点才能把完整的“抛物线”圆滑地画出来,一般区5个点以上,顶点是中心点。(3)巩固练习:画出的图象,并用简洁的语言描述图象的性质。(可以用小组讨论的形式来讨论他们性质。)(4)小结:简单复述本节主题内容(略)(5)作业:P153(1)(3)oy-4-3-2-1123123-2-3-4-5-6x