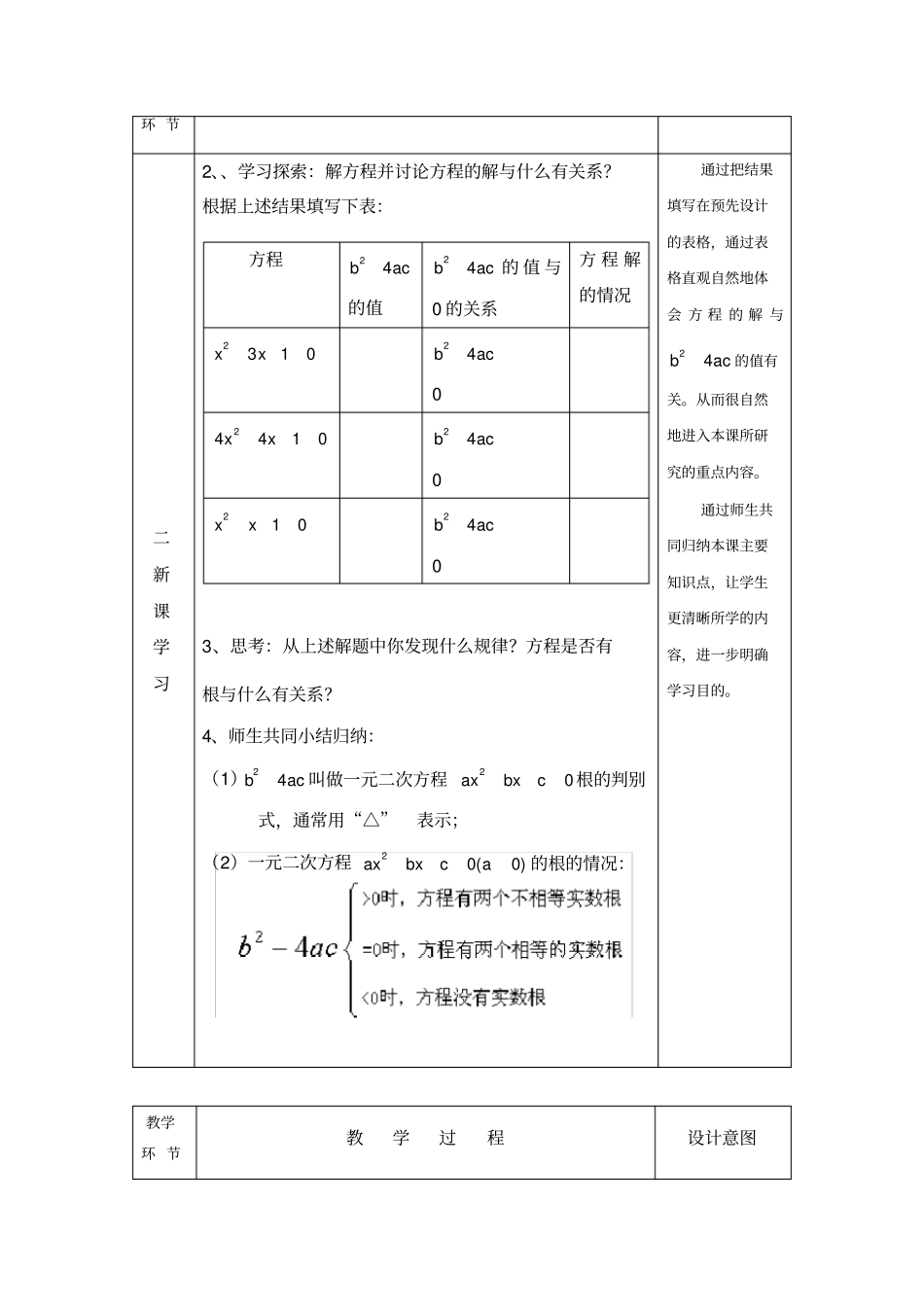
《一元二次方程的根的判别式》教学设计一、教学目标目标(一)知识教学点:1.了解根的判别式的概念,2.能用判别式判别根的情况。(二)能力训练点:1.培养学生从具体到抽象的观察、分析、归纳的能力。2.进一步考察学生思维的全面性。(三)德育渗透点:1.通过了解知识之间的内在联系,培养学生的探索精神。2.进一步渗透转化和分类的思想方法。二、教学重点:会用判别式判定根的情况。三、教学步骤:教学环节教学过程设计意图一复习引入1、用公式法解方程:(1)2310xx解:∵a=,b=,c=∴24bac=()2-4×()×()=+=>0∴242bbacxa=()2()=()()()∴1x=;2x=;(2)24410xx(3)210xx为了让学生能自主地体会“方程的解与什么有关系?”,让学生能把新知识当旧知识来理解,在学习新知前,先让学生解方程,通过练习来复习用公式法解方程,教学教学过程设计意图环节二新课学习2、、学习探索:解方程并讨论方程的解与什么有关系?根据上述结果填写下表:3、思考:从上述解题中你发现什么规律?方程是否有根与什么有关系?4、师生共同小结归纳:(1)24bac叫做一元二次方程20axbxc根的判别式,通常用“△”表示;(2)一元二次方程20(0)axbxca的根的情况:方程24bac的值24bac的值与0的关系方程解的情况2310xx24bac024410xx24bac0210xx24bac0通过把结果填写在预先设计的表格,通过表格直观自然地体会方程的解与24bac的值有关。从而很自然地进入本课所研究的重点内容。通过师生共同归纳本课主要知识点,让学生更清晰所学的内容,进一步明确学习目的。教学环节教学过程设计意图二新课学习5、例题讲解:根的判别式的应用:例1:不解方程,判别方程01232xx的根的情况强调两点:(1)只要能判别△值的符号就行,具体数值不必计算出。(2)判别根的情况,不必求出方程的根。例2:已知关于x的方程0)12(22kxkx,当k取什么值时方程有两个相等的实数根?例题的分析和讲解让学生明确学习根的判别式的作用,学会怎样借助根的判别式解决有关的问题。三课堂分层训练A组不解方程,判别下列方程的根的情况(1)22340xx解:∵a=,b=,c=∴△=24bac=()2-4×()×()=+=∴原方程实数根。(2)29412yy解:原方程可变形为:∵a=,b=,c=∴△=24bac==∴原方程实数根。安排分层练习,满足不同层次学生的学习需求。A组题以基础为主,要求全体同学必须掌握。。教学环节教学过程设计意图四课堂分(3)25(1)70xx解:B组B组要求层训练1、已知关于x的方程223230xkxkk,当k取什么值时方程有两个相等的实数根?(分析:方程有两个相等的实数根,即24bac)解:∵a=,b=,c=∴24bac=()2-4×()×()=∵方程有两个相等的实数根;∴△=24bac___0∴∴k=2、k是什么实数时,方程22(21)0xkxk没有实数根?解:3、k是什么实数时,方程2(21)0kxkxk有两个不相等的实数根?解:60%左右的同学完成。其中最后一题由数字系数,过渡到字母系数,使学生体会到由具体到抽象,并且注意字母的取值教学环节教学过程设计意图四课堂训练C组1、判别关于x的方程22(21)10kxkx的根的情况。C组要求学有余力的同学自觉完成2、若关于x的方程2211kxkxxxxx只有一个解,试求k的值及方程的解。五课堂小结1、判别式的意义及一元二次方程根的情况。①定义:把叫做一元二次方程的根的判别式。用“△”表示②一元二次方程。当△>0时,有两个不相等的实数根;当△=0时,有两个相等的实数根;当△<0时,没有实数根。反之亦然。2、通过根的情况的研究过程,深刻体会转化的思想方法及分类的思想方法。最后的课堂小结再一次地理顺本课的思路。