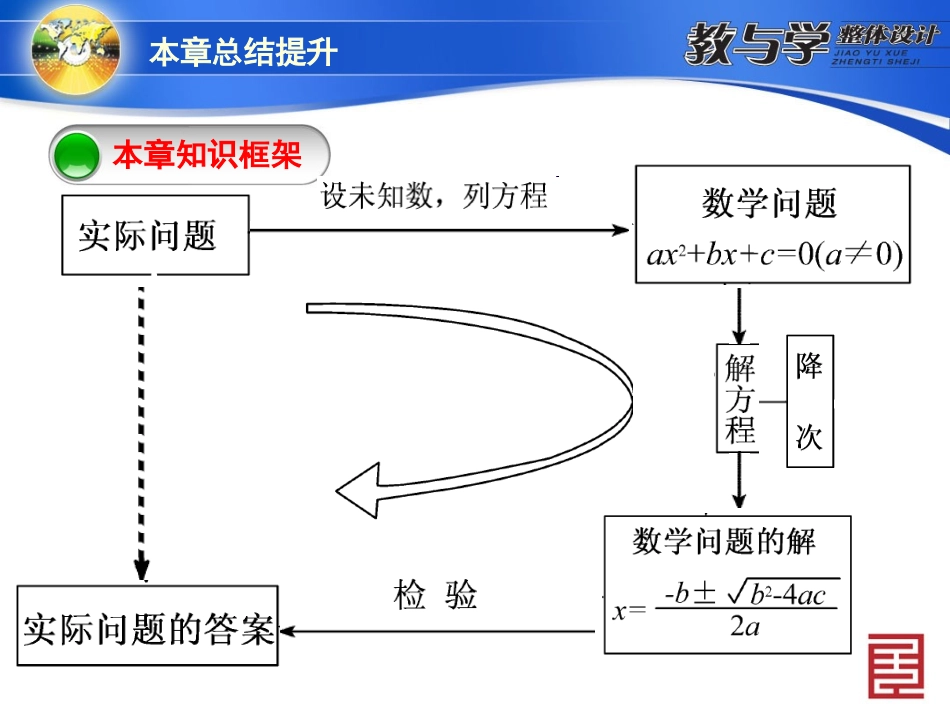
数学新课标(RJ)九年级上册本章总结提升本章知识框架本章知识框架整合拓展创新整合拓展创新本章知识框架本章总结提升x=-b+b2-4ac2a不相等相等无-baca本章总结提升整合拓展创新►探究问题一一元二次方程及有关概念本章总结提升一元二次方程必须满足三个条件:①整式方程;②含一个未知数;③经化简后未知数的最高次数是2.一元二次方程的一般形式是ax2+bx+c=0(a≠0),在解题中一定要注意隐含条件a≠0.本章总结提升例1关于x的一元二次方程(m+1)xm2+1+4x+2=0的解为()A.x1=1,x2=-1B.x1=x2=1C.x1=x2=-1D.无解[解析]根据题意,得m2+1=2,m+1≠0.∴m=1.∴原方程可化为2x2+4x+2=0,即x2+2x+1=0,(x+1)2=0,∴x1=x2=-1.C[点评]掌握一元二次方程的概念是解本题的关键.本章总结提升例2关于x的一元二次方程(a-1)x2+x+a2+2a-3=0的一个根是0,则a=.-3[解析]把0代入一元二次方程(a-1)x2+x+a2+2a-3=0即可得到关于a的一元二次方程a2+2a-3=0,从而求得a1=1,a2=-3,但二次项的系数a-1≠0,即a≠1,所以a=-3.[点评]将已知一元二次方程的根代入方程中即可求出字母系数的值,但要注意二次项系数不为零这一隐含条件.【针对训练】本章总结提升1.若方程(m-1)x2+mx=1是关于x的一元二次方程,则m的取值范围是()A.m≠1B.m≥0C.m≥0且m≠1D.m为任意实数[解析]由题意知m≥0,m-1≠0,解得m≥0且m≠1.C[点评]应注意m中的“m≥0”.本章总结提升►探究问题二用合适的方法解一元二次方程解一元二次方程常用的方法有:直接开平方法,配方法,公式法,因式分解法等.其中配方法和公式法适合于所有的一元二次方程,而直接开平方法和因式分解法适合于某些特殊的一元二次方程.例3解下列一元二次方程.(1)(x+2)2=25;(2)3x2-6x+1=0;(3)x(x-5)=x-5.[解析](1)用直接开平方法简便;(2)用公式法简便;(3)用因式分解法简便.本章总结提升解:(1)两边直接开平方,得x+2=±5,∴x+2=5或x+2=-5,∴x1=3,x2=-7.(2)a=3,b=-6,c=1,Δ=b2-4ac=(-6)2-4×3×1=36-12=24>0.∴x=6±242×3=6±266=3±63.∴x1=3+63,x2=3-63.(3)移项,得x(x-5)-(x-5)=0,提公因式,得(x-5)(x-1)=0,∴x-5=0或x-1=0,∴x1=5,x2=1.【针对训练】本章总结提升2.方程x(x-1)=x的解是.x1=0,x2=2[解析]x2-x=x,∴x2-2x=0,∴x(x-2)=0,∴x1=0,x2=2.[点评]本题易漏掉解x=0,注意一元二次方程若有实数解,则一定有两个解:两个相等的解或两个不相等的解.本章总结提升3.解方程:t2+2=42t.解:原方程化为一般形式为t2-42t+2=0. a=1,b=-42,c=2,∴b2-4ac=(-42)2-4×1×2=32-8=24>0,∴t=42±262=22±6.∴t1=22+6,t2=22-6.本章总结提升4.用配方法解一元二次方程:x2-2x-2=0.解:x2-2x=2,x2-2x+1=2+1,即(x-1)2=3,∴x-1=±3,∴x1=1+3,x2=1-3.本章总结提升►探究问题三一元二次方程根的判别式及根与系数的关系设一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-ba,x1x2=ca.当b2-4ac>0时,方程有两个不相等的实数根;当b2-4ac=0时,方程有两个相等的实数根;当b2-4ac<0时,方程没有实数根.例4已知关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2.(1)求实数m的取值范围;(2)当x21-x22=0时,求m的值.本章总结提升[解析](1)根据根的判别式Δ≥0,得关于m的不等式求解m.(2)由x21-x22=0得(x1+x2)(x1-x2)=0,得出x1+x2=0或x1-x2=0,利用根与系数的关系、根的判别式分类讨论求解.解:(1)由题意有Δ=(2m-1)2-4m2≥0,解得m≤14.即实数m的取值范围是m≤14.本章总结提升(2)由x21-x22=0得(x1+x2)(x1-x2)=0.若x1+x2=0,即-(2m-1)=0,解得m=12. 12>14,∴m=12不合题意,舍去.若x1-x2=0,即x1=x2,∴Δ=0,由(1)知m=14.故当x21-x22=0时,m=14.【针对训练】本章总结提升5.[2013·孝感]已知关于x...