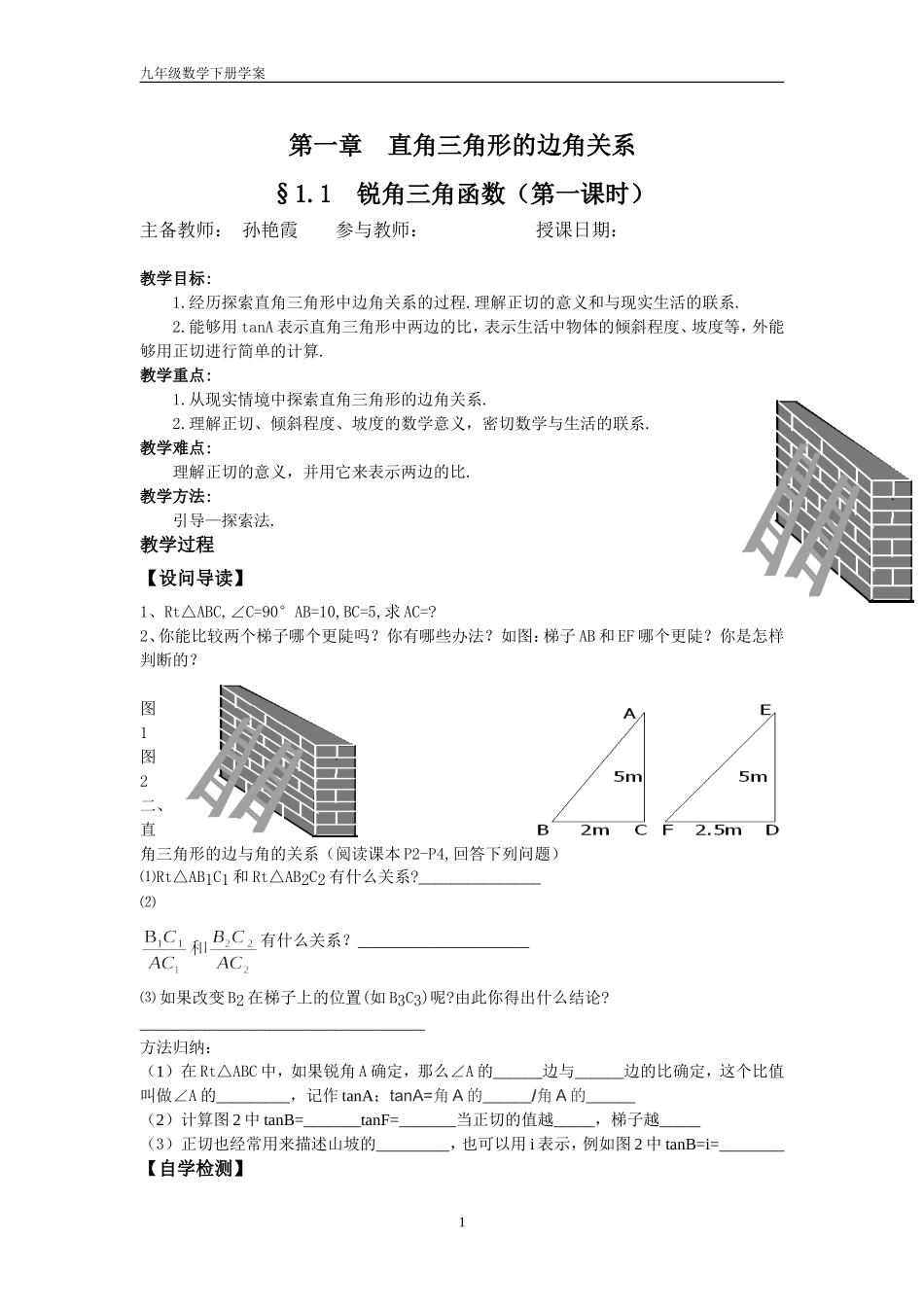
九年级数学下册学案第一章直角三角形的边角关系§1.1锐角三角函数(第一课时)主备教师:孙艳霞参与教师:授课日期:教学目标:1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系.2.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,外能够用正切进行简单的计算.教学重点:1.从现实情境中探索直角三角形的边角关系.2.理解正切、倾斜程度、坡度的数学意义,密切数学与生活的联系.教学难点:理解正切的意义,并用它来表示两边的比.教学方法:引导—探索法.教学过程【设问导读】1、Rt△ABC,∠C=90°AB=10,BC=5,求AC=?2、你能比较两个梯子哪个更陡吗?你有哪些办法?如图:梯子AB和EF哪个更陡?你是怎样判断的?图1图2二、直角三角形的边与角的关系(阅读课本P2-P4,回答下列问题)⑴Rt△AB1C1和Rt△AB2C2有什么关系?_______________⑵有什么关系?_____________________⑶如果改变B2在梯子上的位置(如B3C3)呢?由此你得出什么结论?___________________________________方法归纳:(1)在Rt△ABC中,如果锐角A确定,那么∠A的______边与______边的比确定,这个比值叫做∠A的_________,记作tanA;tanA=角A的______/角A的______(2)计算图2中tanB=_______tanF=_______当正切的值越_____,梯子越_____(3)正切也经常用来描述山坡的_________,也可以用i表示,例如图2中tanB=i=________【自学检测】1九年级数学下册学案1、如图是甲,乙两个自动扶梯,哪一个自动扶梯比较陡?2、在△ABC中,∠C=90°,BC=12cm,AB=20cm,求tanA=______tanB=______3、如图,某人从山脚下的点A走了200m后到达山顶的点B,已知点B到山脚的垂直距离为50m,求山的坡度.【巩固练习】1、如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗?2、菱形的两条对角线分别是16和12.较长的一条对角线与菱形的一边的夹角为θ,则tanθ=______.3、若某人沿坡度i=3:4的斜坡前进10米,则他所在的位置比原来的位置升高________米.【拓展练习】1、如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡比为1:1.5的斜坡AD,求DB的长.(结果保留2九年级数学下册学案根号)2、我们知道山坡的坡角越大,则坡越陡,联想到课本中的结论:tanA的值越大,则坡越陡,我们会得到一个锐角逐渐变大时,它的正切值随着这个角的变化而变化的规律,请你写出这个规律:_____________.【课堂小结】俩人小组互述今天的收获【作业布置】课本第5页第四题3