九年级数学4月月考试卷试卷VIP免费

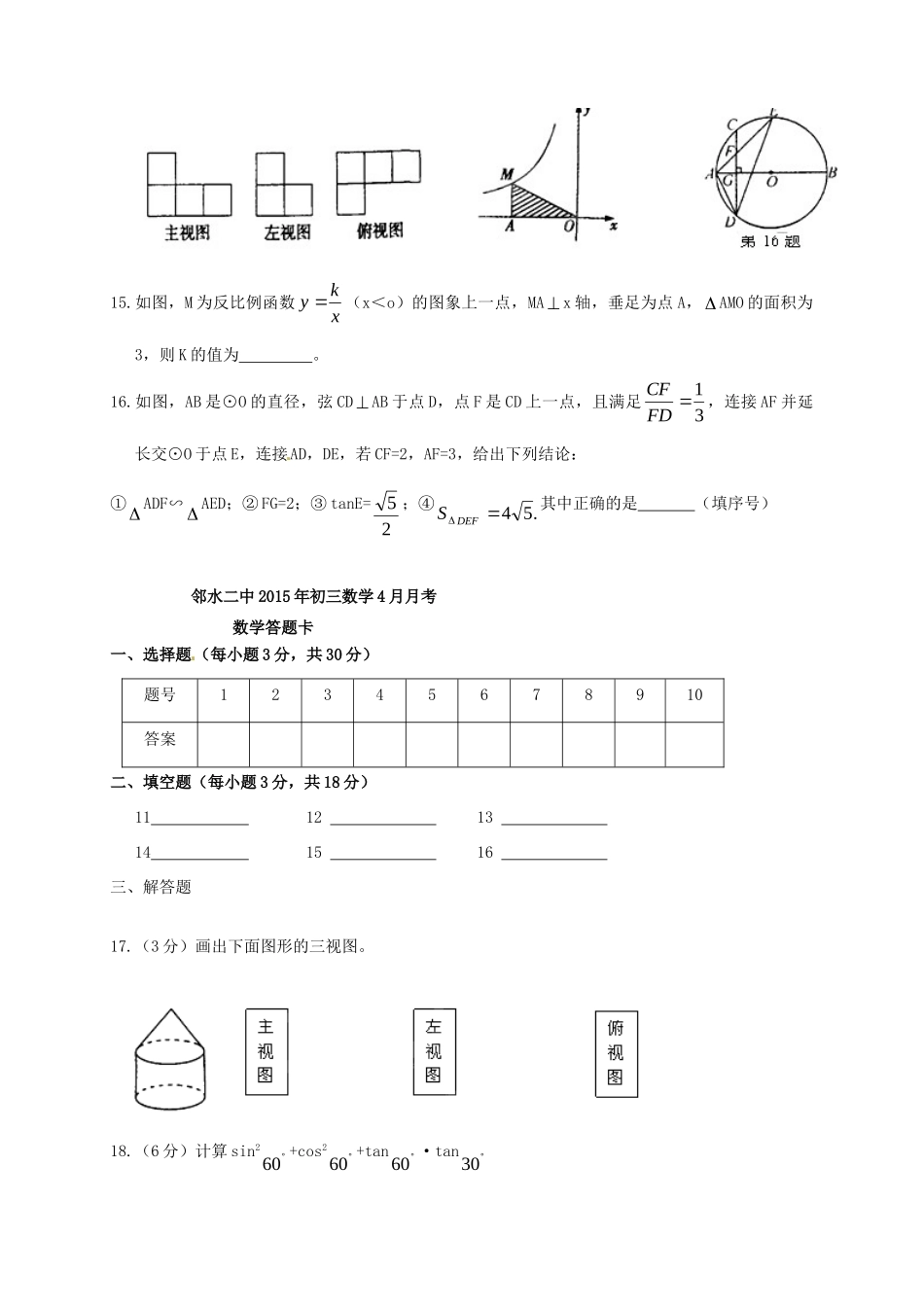
第14题图四川省邻水县第二中学2015届九年级数学4月月考试题一、选择题（每小题3分，共30分）1.如图所示物体的俯视图是（）2.若bbaba则,52=（）A.57B.52C.32D.753.反比例函数xky1的图像位于第一、三象限，则K的取值可能是（）A.-1B.0C.1D.24.如右图小明在打网球时，使球恰好能打过网，而且落点恰好在离网6米的位置上，则球拍击球的高度h为（）A.158米B.1米C.34米D.58米5.已知ABC的三边长分别为4，3，6，与它相似的DEF的最小边长为12，则DEF的周长为（）A.39B.26C.52D.136.等腰三角形的底边长10m，周长为36cm，则底角的正弦值为（）A.185B.165C.1513D.13127.在ABC中，若COSA—21+2tan1B=0，则C的度数是（）A.45B.60C.75D.1058.当＜k0时，反比例函数xky和一次函数2kxy的大致图象是（）9.如图，ABC中，CDAB，垂足为D，下列条件中：①A+B=90；②AB2=AC2+BC2；③BDCDABAC；④CD2=AD·BD，能证明ABC是直角三角形的有（）A.1个B.2个C.3个D.4个10.如图，在中，E，F分别是边AD，BC的中点，AC分别交BE，DF于点M，N，给出下列结论：①ABM≌CDN；②AM=31AC；③DN=2NF；④ABCAMBSS21，中正确的有（）A.1个B.2个C.3个D.4个二、填空题（每小题3分，共18分）11.在RtABC中，ABC=90，AB=4，则sinA=。12.点M（-sin60，COS60）关于X轴对称的点的坐标是。13.在某一时刻，测得身高为1.5m的小明的影长为3m，同时测得一幢高楼的影长为90m，则这幢高楼的高度为m。14.如图是由几个相同的小立方块搭成的几何体的三视图，则搭成这个几何体的小立方块的个数是。15.如图，M为反比例函数xky（x＜o）的图象上一点，MAx轴，垂足为点A，AMO的面积为3，则K的值为。16.如图，AB是⊙O的直径，弦CDAB于点D，点F是CD上一点，且满足31FDCF，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3，给出下列结论：①ADF∽AED；②FG=2；③tanE=25；④.54DEFS其中正确的是（填序号）邻水二中2015年初三数学4月月考数学答题卡一、选择题（每小题3分，共30分）二、填空题（每小题3分，共18分）111213141516三、解答题17.（3分）画出下面图形的三视图。18.（6分）计算sin260+cos260+tan60·tan30题号12345678910答案19.（6分）如图所示，D，E是ABC的边AB，AC上的两点，AE：AC=2：3，且AD=10，AB=15，DE=8，求BC的长。20.（6分）如图，在一次助数学课外实践活动中，小文在点C处测得树的顶端A的仰角为37，BC=20m，求树的高度AB。（参考数据：sin370.60，cos370.80，tan370.75）21.（8分）如图，拦水坝的横断面为梯形ABCD，坝顶宽AD=5米，斜坡AB的坡度i=1：3（指坡面的铅直高度AE与水平宽度BE的比）斜坡DC的坡度i=1：1.5，已知该拦水坝的高度为6米。（1）求斜坡AB的长；（2）求拦水坝的横断面积梯形ABCD的周长。（注意：本题中的计算过程和结果均保留根号）22.（8分）如图，一次函数bkx1y的图象与反比例函数2y=xm的图象相交于点A（2，5）和点B，与y轴相交于点C（0，7）。（1）求这两个函数的解析式；（2）当x取何值为，＜1y2y23.（8分）如图，已知在平面直角坐标系是坐标原点中，OxOy，点A（2，5）在反比例函数xky的图象上，过点A的直线。轴于点交Bxbxy（1）求的值；和bk（2）求OAB的面积。24.（8分）在一次海上搜求行动中，我两艘专业求助船A，B同时收到有关可疑漂浮物的讯息，可疑漂浮物P的求助船A的北偏东5.53方向上，在求助船B的西北方向上，船期B在船A正东方向140海里处.（参考数据：sin5.360.6，cos5.360.8，tan5.360.75）（1）求可疑漂浮物P到A，B两船所在直线的距离；（2）若求助船A，求助船B分别以40海里/时，30海里/时的速度同时出发，匀速直线前往搜求，试通过计算判断哪艘船先到达P处。25.（9分）如图，四边形ABCD中，AC平分DAB，ADC=ACB=90，E为AB的中点.（1）求证：AC2=AB·AD；（2）求证：CE//AD；（3）若AD=4，AB=6，求AFAC的值。26.（10分）如图1，在正方形ABCD中，E，F分别为BC，CD的中点，连接AE，BF，交点为G.（1）求证：AEBF；（2）求证：BCF沿BF对折，得到BPE（如图2），延长FP交BA的延长线于Q，求sinBQP的值；（3）将ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到AHM（如图3），若AM和BF相交于点N，当正方形ABCD的积为4时，求四边形GHMN的面积。