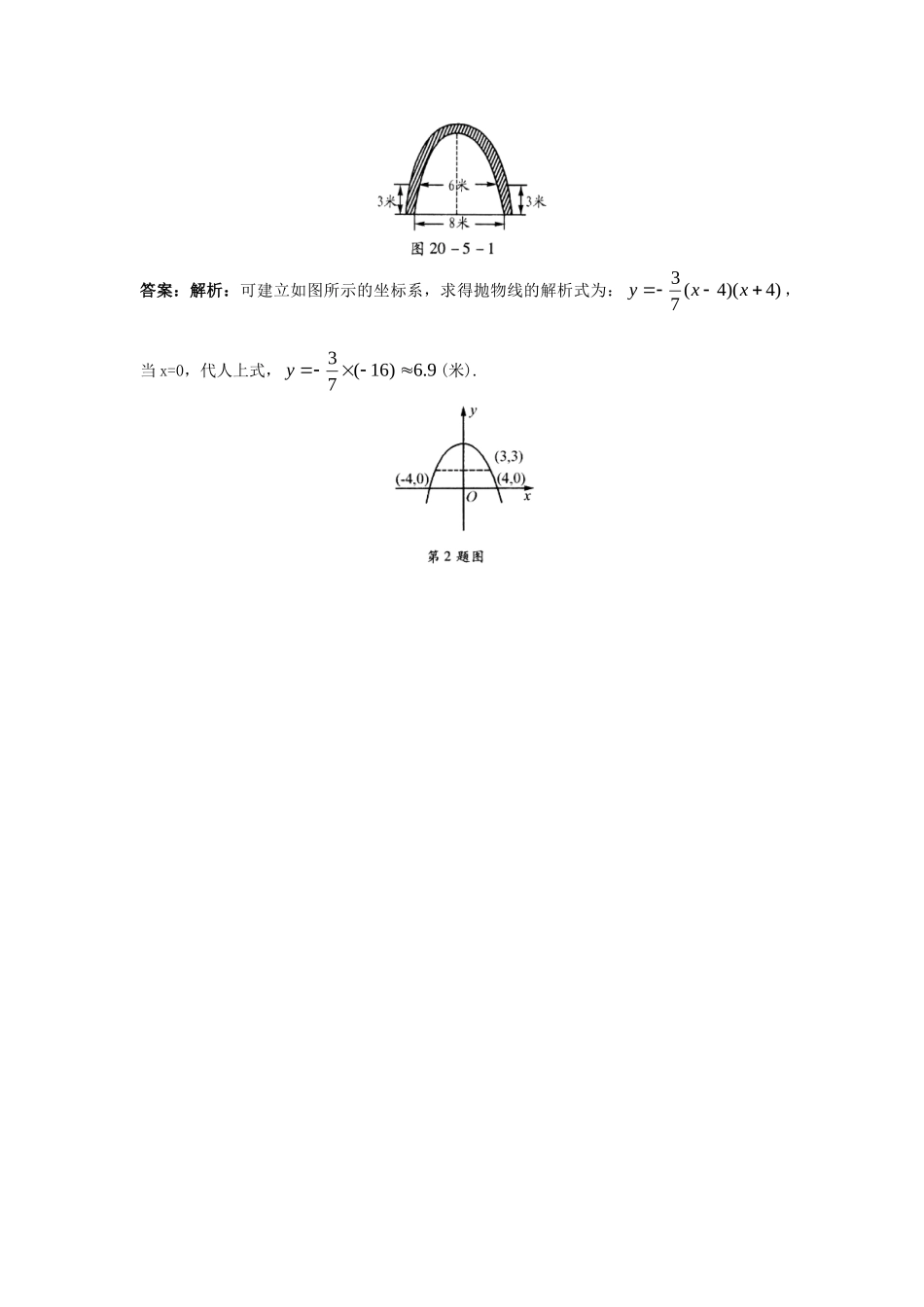
20.5二次函数的一些应用自主学习主干知识←提前预习勤于归纳→认真阅读教材,完成下列问题1.利用二次函数性质判断下列抛物线与x轴的交点情况:(1)y=x2+2x-4(2)y=-2x2+5x-1(3)y=x2+3x+8答案:(1)两个交点(2)两个交点(3)没有交点2.某市近年来经济发展速度很快,根据统计:该市国民生产总值1990年为8.6亿元人民币,1995年为10.4亿元人民币,2000年为12.9亿元人民币.经论证,上述数据适合一个二次函数关系式.请你根据这个函数关系式,预测2005年该市国民生产总值将达到多少?答案:解析:依题意,可以把三组数据看成三个点:A(0,8.6),B(5,10.4),C(10,12.9),设y=ax2+bx+c,把A、B、C三点坐标代人此式,得,9.1210100,4.10525,6.8cbacbac,解得,6.8,29.0,014.0cba即所求二次函数为y=0.014x2+0.29x+8.6.令x=15,代入二次函数关系式,得y=16.1.所以,2005年该市国民生产总值将达到16.1亿元人民币.点击思维←温故知新查漏补缺→1.对于二次函数y=-3x2+2x-5,小明说,无论x取何值时,函数值永远是负值,你同意他的观点吗?为什么?答案:解析:小明的观点是正确的,理由:因为a=-3<0,所以抛物线开口向下,又因为b2-4ac=22-4×(-3)×(-5)<0,所以该抛物线与x轴无交点,所以无论x取何值时,对应的函数值永远是负值.(可结合图象理解)2.某工厂的大门是一抛物线形水泥建筑物(如图20-5-1所示),大门的地面宽度为8米,两侧距地面3米高处各有一壁灯,两壁灯之间的水平距离为6米,则厂门的高为多少米?(水泥建筑物厚度忽略不计,精确到0.1米)答案:解析:可建立如图所示的坐标系,求得抛物线的解析式为:)4)(4(73xxy,当x=0,代人上式,9.6)16(73y(米).