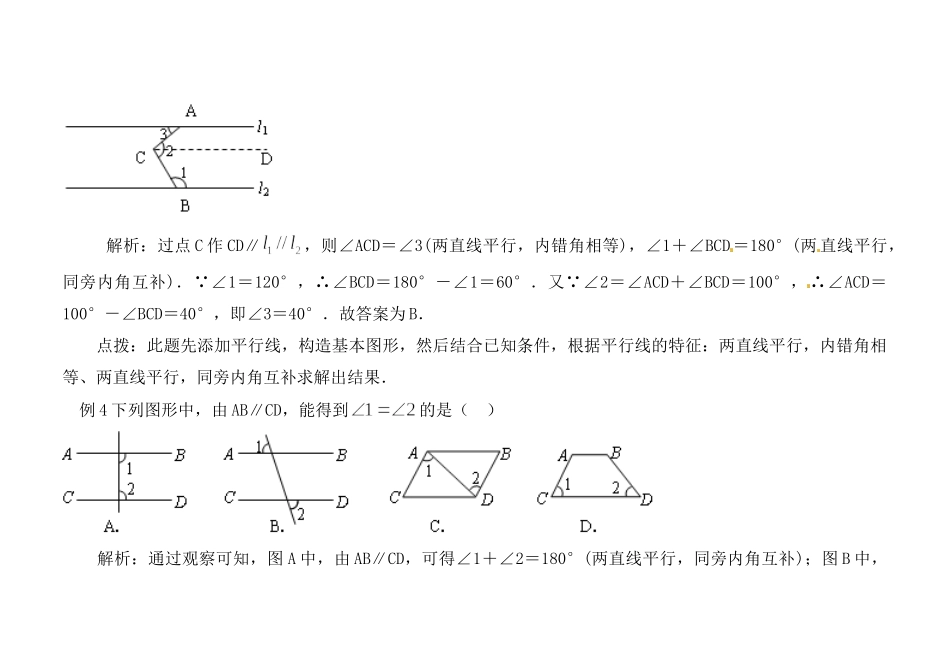
山东省滨州市无棣县埕口中学九年级数学平行线的特征例析掌握好平行线的特征的关键是,熟练地从已知图形中辨别出同位角、内错角、同旁内角,并能迅速地根据平行线的特征,解决求角度问题及角与角的关系问题.例1如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,则∠D=()A.37°B.53°C.60°D.65°解析:∵AB∥CD,∴∠ECD=∠A=37º(两直线平行,同位角相等).又∵∠ECD+∠D=90°,∴∠D=90°-37º=53°.故答案为B.点拨:此题根据平行线的特征:两直线平行,同位角相等,先求出∠ECD,然后再根据直角三角形的两个锐角和等于90°,求解出结果.例2如图,已知∠1=∠2,∠3=80°,则∠4=()A.80°B.70°C.60°D.50°解析:∵∠1=∠2,∠1与∠2的对顶角是内错角,∴a∥b(内错角相等,两直线平行).∴∠3=∠4=80°(两直线平行,内错角相等).故答案为A.点拨:此题利用题目中条件及对顶角相等,可先得出a∥b,然后再根据平行线的特征:两直线平行,内错角相等,得出结论.例3()如图,,∠1=120°,∠2=100°,则∠3=()A.20°B.40°C.50°D.60°解析:过点C作CD∥,则∠ACD=∠3(两直线平行,内错角相等),∠1+∠BCD=180°(两直线平行,同旁内角互补).∵∠1=120°,∴∠BCD=180°-∠1=60°.又∵∠2=∠ACD+∠BCD=100°,∴∠ACD=100°-∠BCD=40°,即∠3=40°.故答案为B.点拨:此题先添加平行线,构造基本图形,然后结合已知条件,根据平行线的特征:两直线平行,内错角相等、两直线平行,同旁内角互补求解出结果.例4下列图形中,由AB∥CD,能得到的是()解析:通过观察可知,图A中,由AB∥CD,可得∠1+∠2=180°(两直线平行,同旁内角互补);图B中,由AB∥CD,可得∠1与∠2的对顶角相等(两直线平行,同位角相等),即∠1=∠2;图C中,由AB∥CD,不能得出∠1=∠2;图D中,由AB∥CD,也不能得出∠1与∠2.故答案为B.点拨:此题不仅要熟悉图形,还要善于利用平行线的特征,判断出角与角之间的关系.