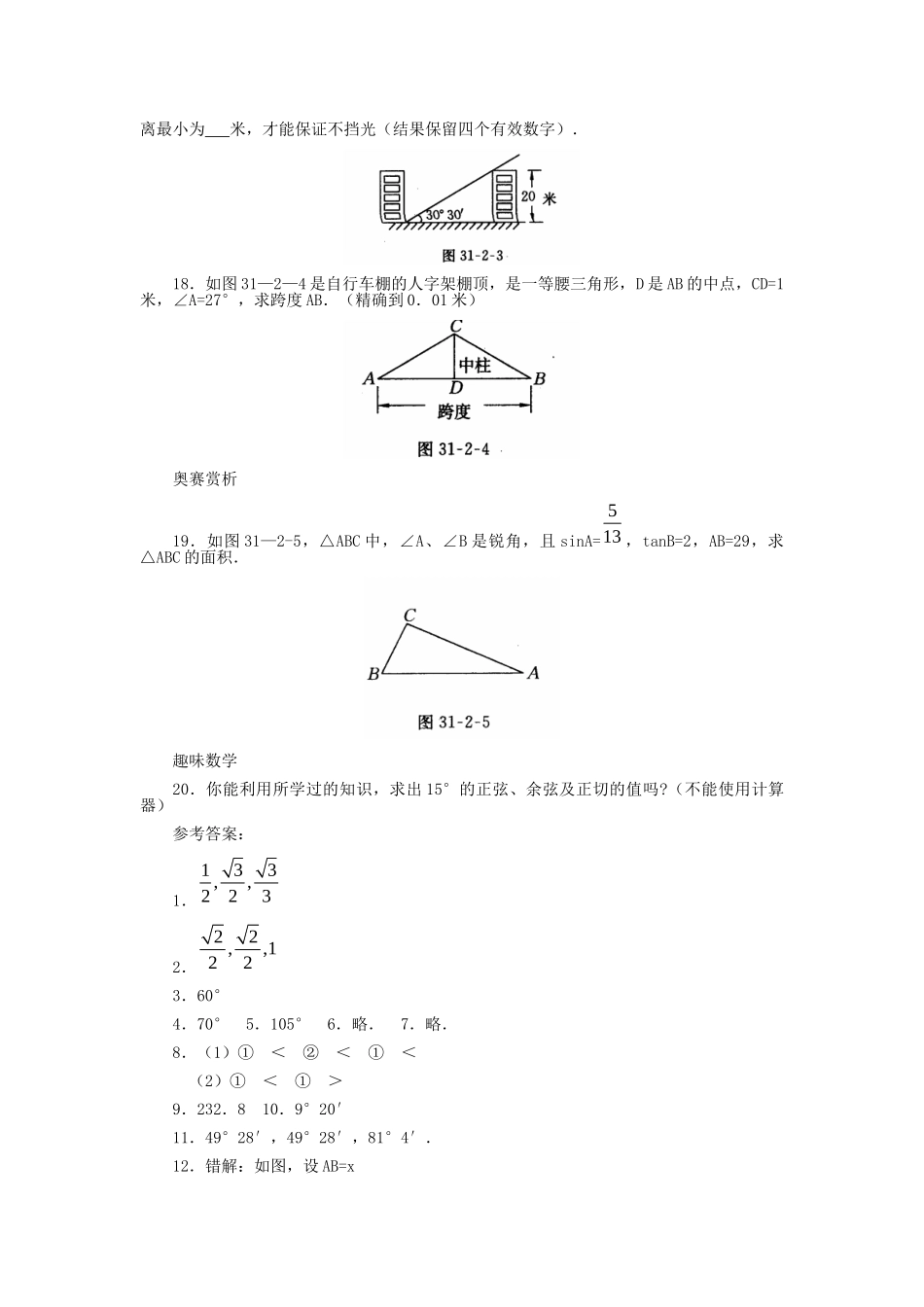
31.2锐角三角函数值的求法习题精选自主演练,各个击破1.sin30°=,cos30°=,tan30°=.2.sin45°=,cos45°=,tan45°=.3.tan3,则=.4.1cos102,则=.5.153sin22x,则x=.6.利用计算器求下列各函数值.(1)sin54°,(2)cos40°,(3)tan38°,(4)sinl7°54′,(5)cos57°32′58″,(6)tan73°20″,(7)sin28.7°—cos54°36′+tan51°47′,(8)tan24.5°·tan65.5°.7.利用计算器求下列各角(精确到1″)(1)sinA=0.75,求A;(2)cosB=0.8889,求B;(3)tanC=45.43,求C;(4)tanD=0.9742,求n互动探究,拓展延伸8.(1)比较大小①cos47°48′cos39°6′;②tan24°7′tan25°7′;③sin42.7°sin52.9°.(2)锐角、满足①sin=0.476,sin=0.5043,则.②cos=0.4376,cos=0.3943,则.9.一人由山脚爬到山顶,先爬30°山坡80m,再爬40°的山坡300m,则山的高度是多少(精确到0.1m).创新思维(一)新型题10.在1:1000的地图上,量得甲、乙两地水平距离为3.7cm,而两地的实际高度差为6m,求甲、乙两地间的坡角(精确到1′).(二)课本习题变式题11.等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到l′).易错题12.由一建筑物AB的顶端测得地面上一点C的俯角是28°37′,C到AB的底端B的距离是42.6m,求建筑物AB的高.(精确到0.1m)难题巧解13.如图31—2—l,△ABC中,∠BAC=45°,AD⊥BC于D,且AD=6,BD=3,求∠C的度数(精确到1°).迁移运用,落实课标数学在经济、科技、生活中的应用14.如图31—2—2,有甲、乙两楼,甲楼高AD是23米,现在想测量乙楼CB的高度,某人在甲楼的楼底A和楼顶D,分别测得乙楼的楼顶B的仰角为65°13'和45°,利用这些数据可求得乙楼的高度为多少米?(结果精确到0.01米)潜能开发15.在△ABC中,∠C=90°,24343bcbc,能否求出∠A的度数?如能就求出来,如不能,说明理由.开放实践16.设为任意锐角,你能否说明tan与sin之间的大小关系?如能,请比较大小,不能,请说明理由.经典名题,提升自我:中考链接17.青岛位于北纬36°4′,通过计算可以求得:在冬至日正午时的太阳人射角为30°30′(如图31—2—3所示).因此,在规划建设楼高为20米的小区时,两楼间的距离最小为米,才能保证不挡光(结果保留四个有效数字).18.如图31—2—4是自行车棚的人字架棚顶,是一等腰三角形,D是AB的中点,CD=1米,∠A=27°,求跨度AB.(精确到0.01米)奥赛赏析19.如图31—2-5,△ABC中,∠A、∠B是锐角,且sinA=513,tanB=2,AB=29,求△ABC的面积.趣味数学20.你能利用所学过的知识,求出15°的正弦、余弦及正切的值吗?(不能使用计算器)参考答案:1.133,,2232.22,,1223.60°4.70°5.105°6.略.7.略.8.(1)①<②<①<(2)①<①>9.232.810.9°20′11.49°28′,49°28′,81°4′.12.错解:如图,设AB=x∴∠CAB=28°37′,CB=42.6,正解:设AB=x,则∠DAC=28°37′,∴∠ACB=28°37′,∴42.678.1tan2837'xm解得x=42.6×tan28°37′≈23.2(m).13.在Rt△∠ADB中,AD=6,BE=3.∴tanB=2,∠B≈63.4°.∴∠C=72°.14.42.73米.15.能.∵4b2+3c2—43bc=0,∴4b2—43bc+3c2=0,∴2230bc,∴23bc,∴3cos2bAc,∴∠A=30°16.tansin由如下:如图,设是Rt△ABC的一个锐角,令∠B=,则tan,sinACACBCAB.17.33.9518.3.93米.19.过C作CD⊥AB,垂足为D.∵5sin13CDAAC,∴设CD=5k.AC=13k(k>0).∵tan2CDBBD.又2212ADACCDk,∴AB=AD+DB=29292k.∴k=2,∴CD=10.∴