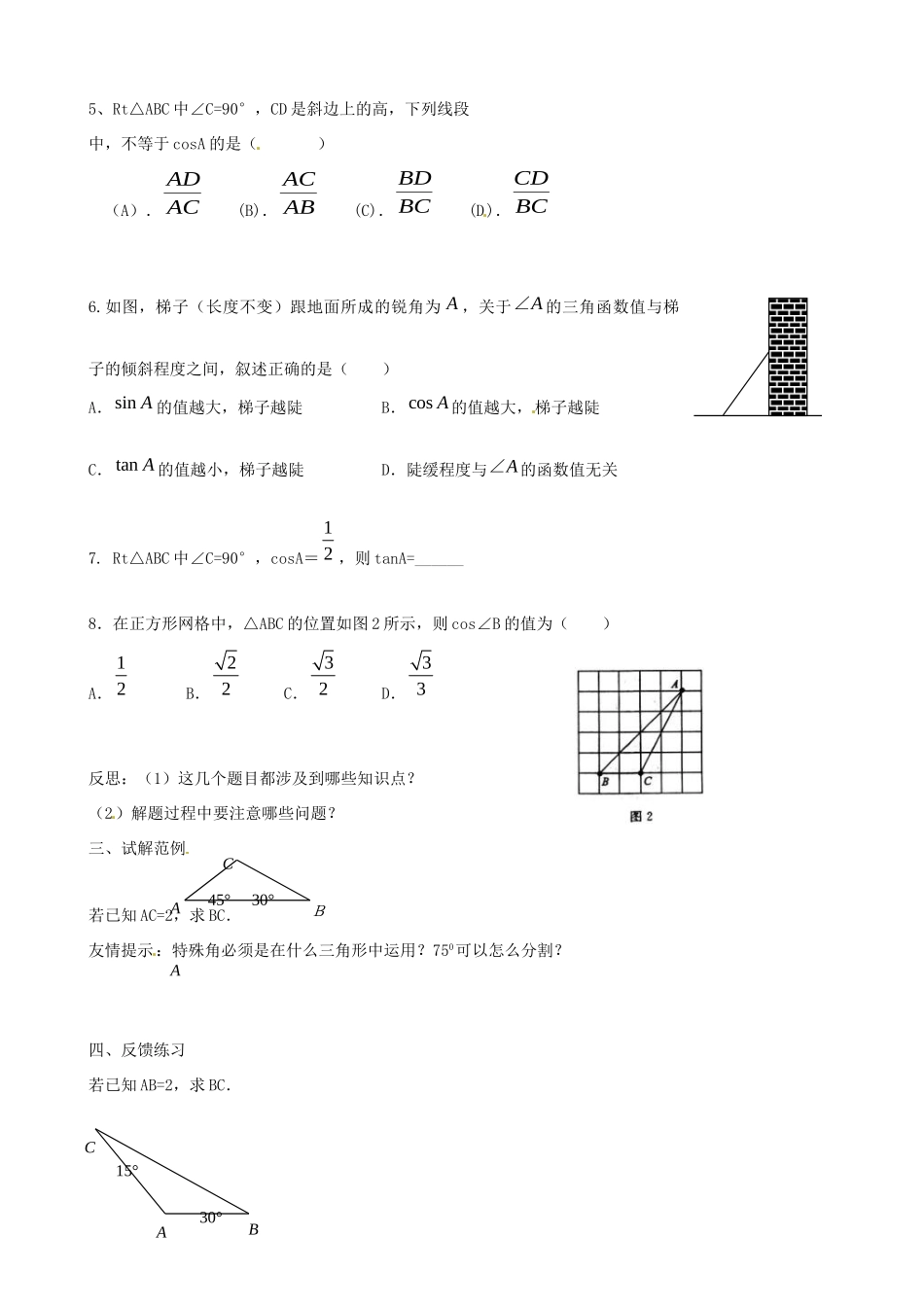
山东省文登市七里汤中学九年级数学《解直角三角形复习》人教新课标版一.补全网络:(一)知识点:(1)由直角三角形中求出的过程.3.解直角三角形三边关系:(2)直角三角形中的边角关系两锐角关系:角与边的关系:友情提示:有关概念和特殊角的函数值要记准有关概念和特殊角的函数值要记准.(二)基本图形:————构造直角三角形1.(1)(2)反思:添加辅助线把一般的三角形分割成直角三角形时要注意什么问题?友情提示:有特殊角的非直角三角形有特殊角的非直角三角形,,常通过作辅助线把它转化为直角三角形来解决常通过作辅助线把它转化为直角三角形来解决,,这种方法叫“化斜为这种方法叫“化斜为直法”直法”,,通常以特殊角为一锐角通常以特殊角为一锐角,,构造直角三角形构造直角三角形.二.巩固网络1、在Rt△ABC中,∠ACB=90°AB=3,BC=2,则sinB=______tanB=______cosB=_____.2、sin30°-tan45°+cos60°cos30°=________.3、等腰三角形的一腰长为2cm,顶角为120°,则底边长为.4、在△ABC中∣sinC—22∣+(23-cosB2)=0则∠A=()(A).100°(B).105°(C).90°(D).60°1.锐角三角函数的意义的意义2.特殊角的三角函数值正弦:sinA=余弦:cosA=正切:tanA=sinαcosαtanα30°45°60°CABBAC15°30°AAB45°30°CCABcba5、Rt△ABC中∠C=90°,CD是斜边上的高,下列线段中,不等于cosA的是()(A).ACAD(B).ABAC(C).BCBD(D).BCCD6.如图,梯子(长度不变)跟地面所成的锐角为A,关于A∠的三角函数值与梯子的倾斜程度之间,叙述正确的是()A.sinA的值越大,梯子越陡B.cosA的值越大,梯子越陡C.tanA的值越小,梯子越陡D.陡缓程度与A∠的函数值无关7.Rt△ABC中∠C=90°,cosA=12,则tanA=______8.在正方形网格中,△ABC的位置如图2所示,则cos∠B的值为()A.12B.22C.32D.33反思:(1)这几个题目都涉及到哪些知识点?(2)解题过程中要注意哪些问题?三、试解范例若已知AC=2,求BC.友情提示:特殊角必须是在什么三角形中运用?750可以怎么分割?四、反馈练习若已知AB=2,求BC.AAB45°30°CBAC15°30°友情提示:解直角三角形时经常要用到方程或方程组来解决问题解直角三角形时经常要用到方程或方程组来解决问题.回思:通过反馈练习你对这类题辅助线的添加有什么收获?五、回顾反思(1)本节课都应用了哪些知识点?(2)解直角三角形的关键是什么?(3)如何利用已知条件构造直角三角形?常用的辅助线是什么?(4)本节涉及哪种数学思想?用到什么具体方法?(5)在学习过程中你认为在哪些方面还存在困惑?