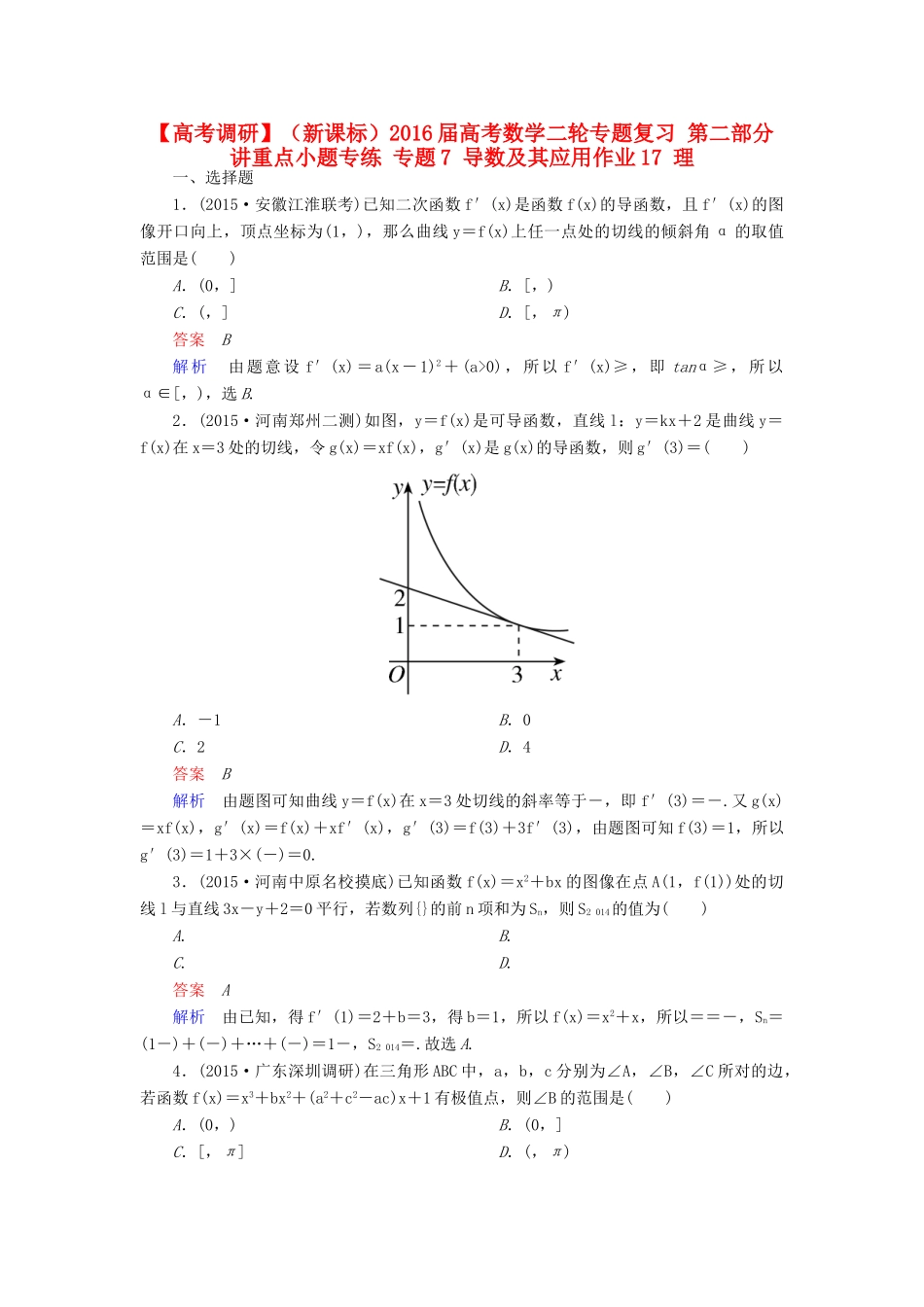
【高考调研】(新课标)2016届高考数学二轮专题复习第二部分讲重点小题专练专题7导数及其应用作业17理一、选择题1.(2015·安徽江淮联考)已知二次函数f′(x)是函数f(x)的导函数,且f′(x)的图像开口向上,顶点坐标为(1,),那么曲线y=f(x)上任一点处的切线的倾斜角α的取值范围是()A.(0,]B.[,)C.(,]D.[,π)答案B解析由题意设f′(x)=a(x-1)2+(a>0),所以f′(x)≥,即tanα≥,所以α∈[,),选B.2.(2015·河南郑州二测)如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),g′(x)是g(x)的导函数,则g′(3)=()A.-1B.0C.2D.4答案B解析由题图可知曲线y=f(x)在x=3处切线的斜率等于-,即f′(3)=-.又g(x)=xf(x),g′(x)=f(x)+xf′(x),g′(3)=f(3)+3f′(3),由题图可知f(3)=1,所以g′(3)=1+3×(-)=0.3.(2015·河南中原名校摸底)已知函数f(x)=x2+bx的图像在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{}的前n项和为Sn,则S2014的值为()A.B.C.D.答案A解析由已知,得f′(1)=2+b=3,得b=1,所以f(x)=x2+x,所以==-,Sn=(1-)+(-)+…+(-)=1-,S2014=.故选A.4.(2015·广东深圳调研)在三角形ABC中,a,b,c分别为∠A,∠B,∠C所对的边,若函数f(x)=x3+bx2+(a2+c2-ac)x+1有极值点,则∠B的范围是()A.(0,)B.(0,]C.[,π]D.(,π)答案D解析若函数f(x)=x3+bx2+(a2+c2-ac)x+1有极值点,则f′(x)=x2+2bx+a2+c2-ac=0有两个不相等的实数根.故Δ=4b2-4(a2+c2-ac)>0,即a2+c2-b2
1时,若y=loga(x+4)的图像经过该平面区域,须10,所以f(x)在R上单调递增,f(0)=1>0,f(-1)=1-1---…-<0,所以f(x)=0的零点在(-1,0)上.而g′(x)=-<0,所以g(x)在R上单调递减,g(0)=1>0,g(1)=1-1+-+-…->0,g(2)=1-2+-+-…-<0,所以g(x)的零点在(1,2)上.设函数F(x)=f(x+3)·g(x-4),且函数F(x)的零点均在区间[a,b](a0,若a=f(),b=-2f(-2),c=(ln)·f(ln),则a,b,c的大小关系正确的是()A.a0时,h′(x)=f(x)+x·f′(x)>0,∴此时函数h(x)单调递增. a=f()=h(),b=-2f(-2)=2f(2)=h(2),c=(ln)f(ln)=h(ln)=h(-ln2)=h(ln2),又0,则不等式(x+2015)3f(x+2015)+27f(-3)>0的解集为()A.(-2018,-2015)B.(-∞,-2016)C.(-2016,-2015)D.(-∞,-2012)答案A解析由题可知,x<0,3f(x)+xf′(x)>0,则3x2f(x)+x3f′(x)>0,即[x3f(x)]′>0,设F(x)=x3f(x),即F′...