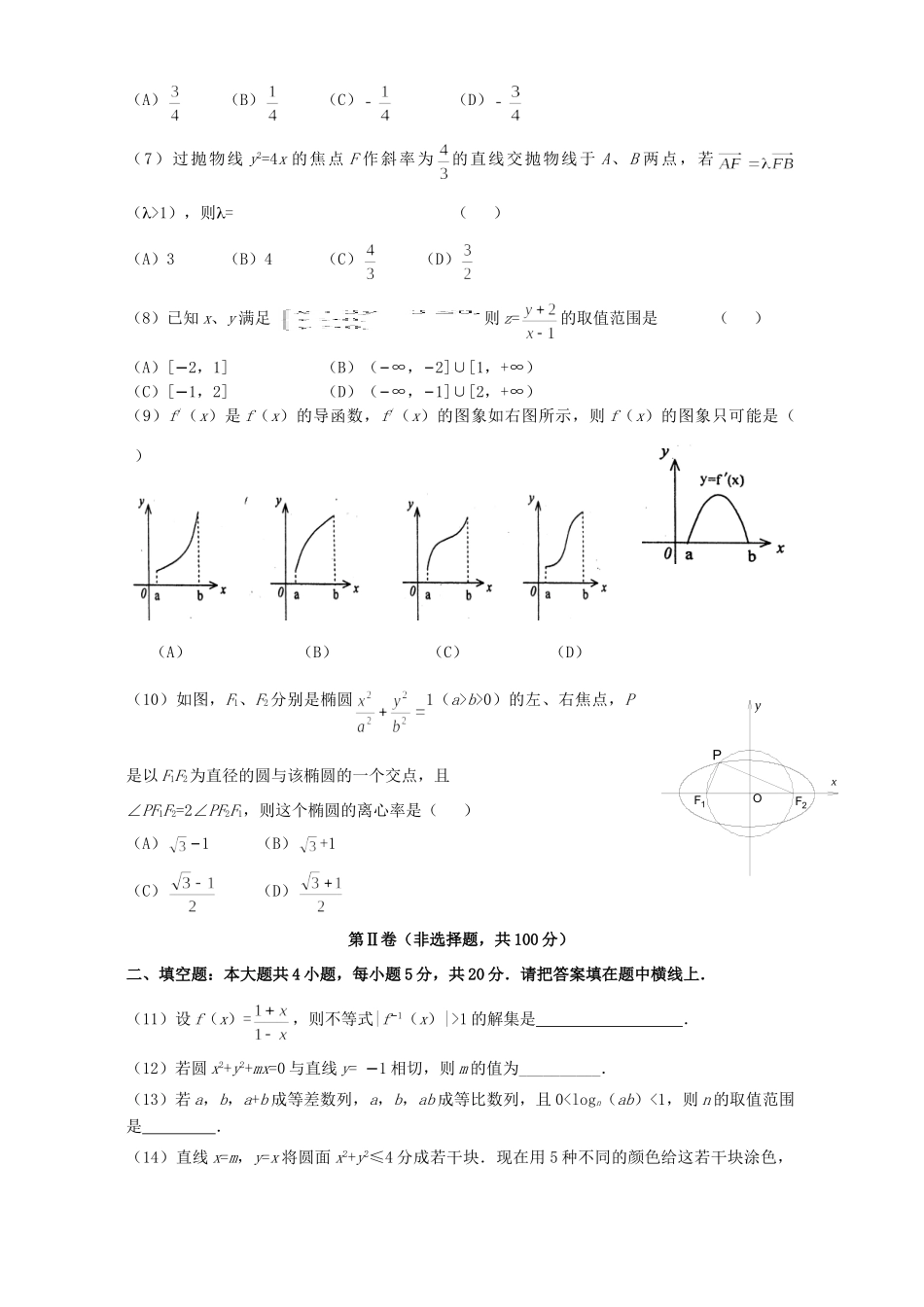
2007届四川成都四中高三数学第三轮复习考试卷三参考公式:如果事件A、B互斥,那么球的表面积公式S=4πR2P(A+B)=P(A)+P(B)如果事件A、B相互独立,那么其中R表示球的半径P(A·B)=P(A)·P(B)球的体积公式如果事件A在一次试验中发生的概率是V=πR3P,那么n次独立重复试验中恰好发生k其中R表示球的半径次的概率第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把答案填在题后的括号内.(1)给出两个命题:p:|x|=x的充要条件是x为正实数;q:存在反函数的函数一定是单调函数.则下列复合命题中是真命题的是()(A)p且q(B)p或q(C)﹁p且q(D)﹁p或q(2)已知sinθ=−,θ∈(−,0),则cos(θ−)的值为()(A)−(B)(C)−(D)(3)若lga+lgb=0(其中a≠1,b≠1),则函数f(x)=ax与g(x)=bx的图象()(A)关于直线y=x对称(B)关于x轴对称(C)关于y轴对称(D)关于原点对称(4)已知直线l、m、n及平面,下列命题中的假命题是()(A)若l//m,m//n,则l//n(B)若l⊥,n//,则l⊥n(C)若l⊥m,m//n,则l⊥n(D)若l//,n//,则l//n(5)定义运算,则符合条件的复数z为()(A)3−i(B)1+3i(C)3+i(D)1−3i(6)已知的展开式的第7项为,则()PF2F1Oyx(A)(B)(C)(D)(7)过抛物线y2=4x的焦点F作斜率为的直线交抛物线于A、B两点,若(>1),则=()(A)3(B)4(C)(D)(8)已知x、y满足则z=的取值范围是()(A)[2−,1](B)(−∞,−2]∪[1,+∞)(C)[1−,2](D)(−∞,−1]∪[2,+∞)(9)f/(x)是f(x)的导函数,f/(x)的图象如右图所示,则f(x)的图象只可能是()(A)(B)(C)(D)(10)如图,F1、F2分别是椭圆1(a>b>0)的左、右焦点,P是以F1F2为直径的圆与该椭圆的一个交点,且∠PF1F2=2∠PF2F1,则这个椭圆的离心率是()(A)−1(B)+1(C)(D)第Ⅱ卷(非选择题,共100分)二、填空题:本大题共4小题,每小题5分,共20分.请把答案填在题中横线上.(11)设f(x)=,则不等式|f−1(x)|>1的解集是.(12)若圆x2+y2+mx=0与直线y=1−相切,则m的值为__________.(13)若a,b,a+b成等差数列,a,b,ab成等比数列,且00恒成立,求实数m的取值范围.(17)(本小题满分14分)箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量分别为2个和3个.(Ⅰ)若从箱中随机取出三个球,求至少取到一个黄球的概率;(Ⅱ)若从箱中每次任意取出一个球,如果取出的是黄球则结束,如果取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过3次.以ξ表示取球结束时已取到白球的次数.求ξ的分布列与数学期望;(Ⅲ)在(Ⅱ)中,如果不限定取球的次数,若以η表示取球结束时的取球次数,求η的分布列与数学期望.(18)(本小题满分14分)如图,在直三棱柱ABC−A1B1C1中,AC=BC=2,AA1=2,∠ACB=90°,M是AA1的中点,N是BC1中点.(Ⅰ)求证:MN∥平面A1B1C1;(Ⅱ)求点C1到平面BCM的距离;(Ⅲ)求二面角B−C1M−A的大小.(19)(本小题满分14分)已知数列{an}中,a1=1,且点P(an,an+1)(n∈N*)在直线x−y+1=0上.(Ⅰ)若函数f(n)=+++…+(n∈N,且n≥2),求证:f(n)≥;(Ⅱ)设bn=,Sn表示数列{bn}的前n项和.试问...