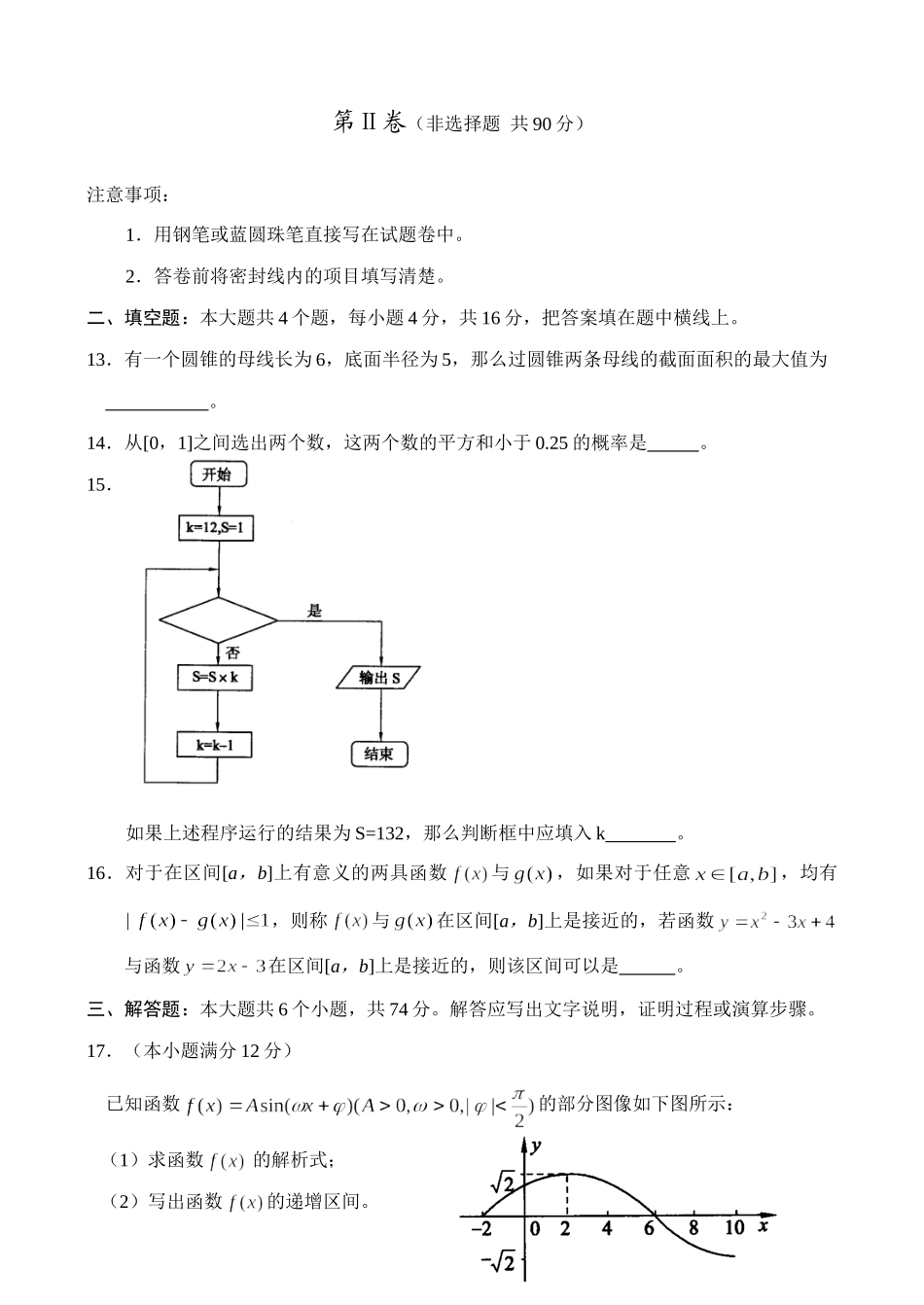
山东省济南市2006-2007学年度第一学期高三数学理工农医类统一考试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,测试时间120分钟。第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个备选项中,只有一项是符合题目要求的。1.设集合,则()A.B.(C.(D.2.是直线和直线垂直的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.要完成下列两项调查:①从某社区125户高收入家庭、280户中等收入家庭、95户低收入人家庭中选出100户调查社会购买力的某项指标;②某中学的15名艺术特长生中选出3人调查学习负担情况。宜采用的抽样方法依次为()A.①用随机抽样法,②用系统抽样法B.①用分层抽样法,②用随机抽样法C.①用系统抽样法,②用分层抽样法D.①②都用分层抽样法4.已知函数是定义R上的奇函数且,当时,那使成立的x的集合为()A.B.C.D.5.已知直线l的方程为:,则l与两坐标轴围成的三角形的内切圆方程为()A.B.C.D.6.已知,若,则的值为()A.B.C.D.7.已知直线与圆交于A,B两点,且,其中O为坐标原点,则实数a的值为()A.2B.-2C.2或-2D.或8.定义运算:,则函数的图象是()9.若向量,且7,那么等于()A.-2B.0C.-2或2D.210.设是空间三条直线,是空间两个平面,则下列命题中,逆命题不成立的是()A.当时,若,则B.当时,若,则C.当,且c是a内的射影时,若,则D.当,且时,,则11.若圆至少能盖住函数的图象的一个最高点和一个最低点,则r的取值范围是()A.B.C.D.以上都不对12.关径为R的球的内接正三棱柱的侧面积(各侧面面积之和)的最大值为()A.B.C.D.第Ⅱ卷(非选择题共90分)注意事项:1.用钢笔或蓝圆珠笔直接写在试题卷中。2.答卷前将密封线内的项目填写清楚。二、填空题:本大题共4个题,每小题4分,共16分,把答案填在题中横线上。13.有一个圆锥的母线长为6,底面半径为5,那么过圆锥两条母线的截面面积的最大值为。14.从[0,1]之间选出两个数,这两个数的平方和小于0.25的概率是。15.如果上述程序运行的结果为S=132,那么判断框中应填入k。16.对于在区间[a,b]上有意义的两具函数与,如果对于任意,均有,则称与在区间[a,b]上是接近的,若函数与函数在区间[a,b]上是接近的,则该区间可以是。三、解答题:本大题共6个小题,共74分。解答应写出文字说明,证明过程或演算步骤。17.(本小题满分12分)已知函数的部分图像如下图所示:(1)求函数的解析式;(2)写出函数的递增区间。18.(本小题满分12分)在正四棱锥S—ABCD中,E、F、G分别是BC、SC和DC的中点,P眯在线段FG上。求证:(1)平面EFG//平面SDB;(2)PE⊥AC。19.(本小题满分12分)某种洗衣机洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程。假设进水时水量匀速增加,清洗时水量保持不变。已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟。洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:x0241616.51718…y020404029.5202…请根据表中提供的信息解答下列问题:(1)试写出当时y关于x的函数解析式,并画出该函数的图象;(2)根据排水阶段的2分钟点(x,y)的分布情况,可选用或(其中a、b、c、d为常数),作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数。试分别求出这两个函数的解析式;20.(本小题满分12分)如图是某多面体的三视图,如果图中每个正方形的边长为2。(1)请描述满足该三视图的一个几何的形状(或画出它的直观图);(2)求你得到的几何体的体积;(3)求你得到几何体的表面积。21.(本小题满分12分)设函数其中(1)求函数的最值;(2)判断,当时,函数在区间内是否存在零点。22.(本小题满分14分)在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示)。将矩形折叠,使A点落在线段DC上。(1)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;(2)设折痕所在直线与y轴交于点F,过点E、D、F...