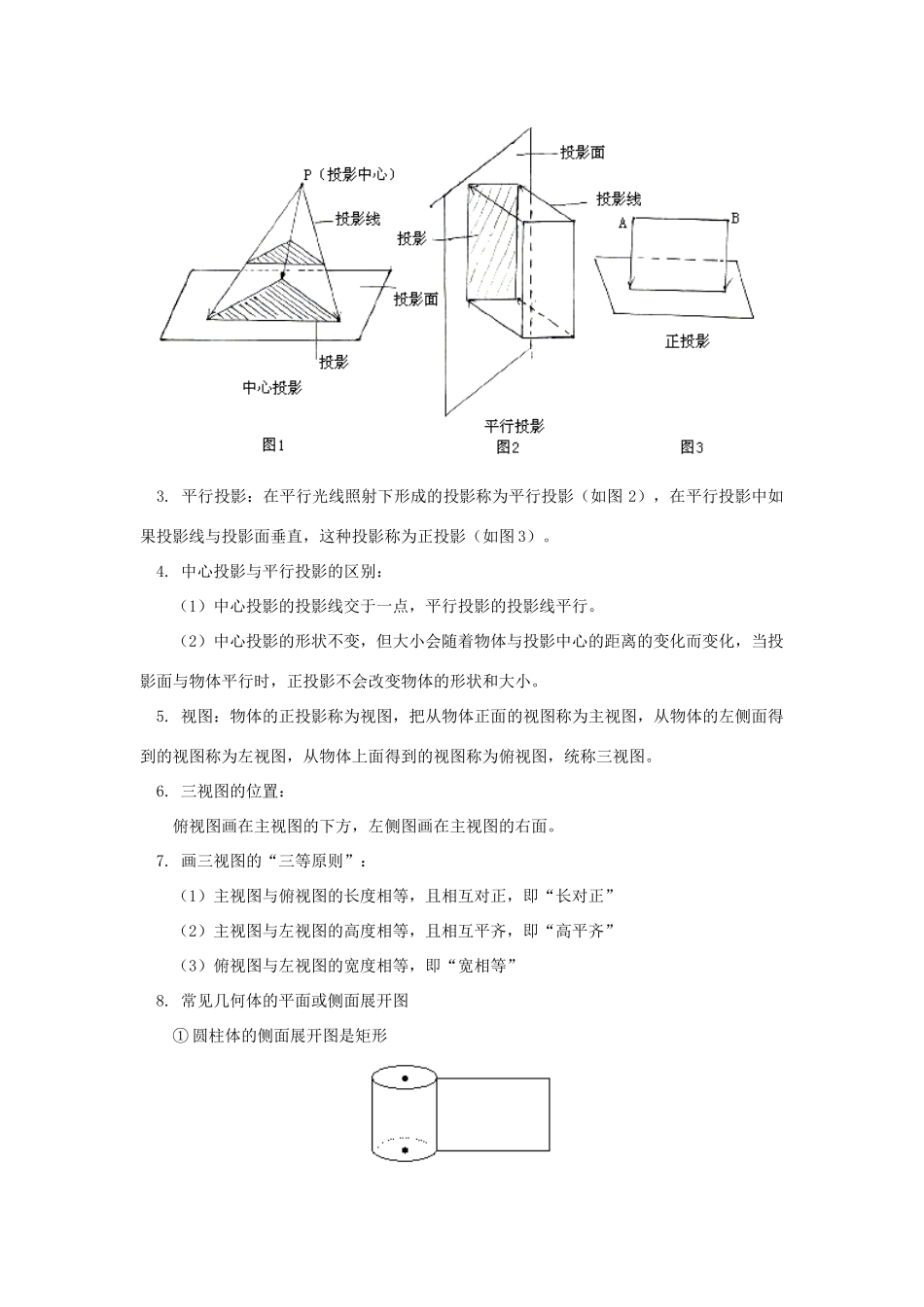
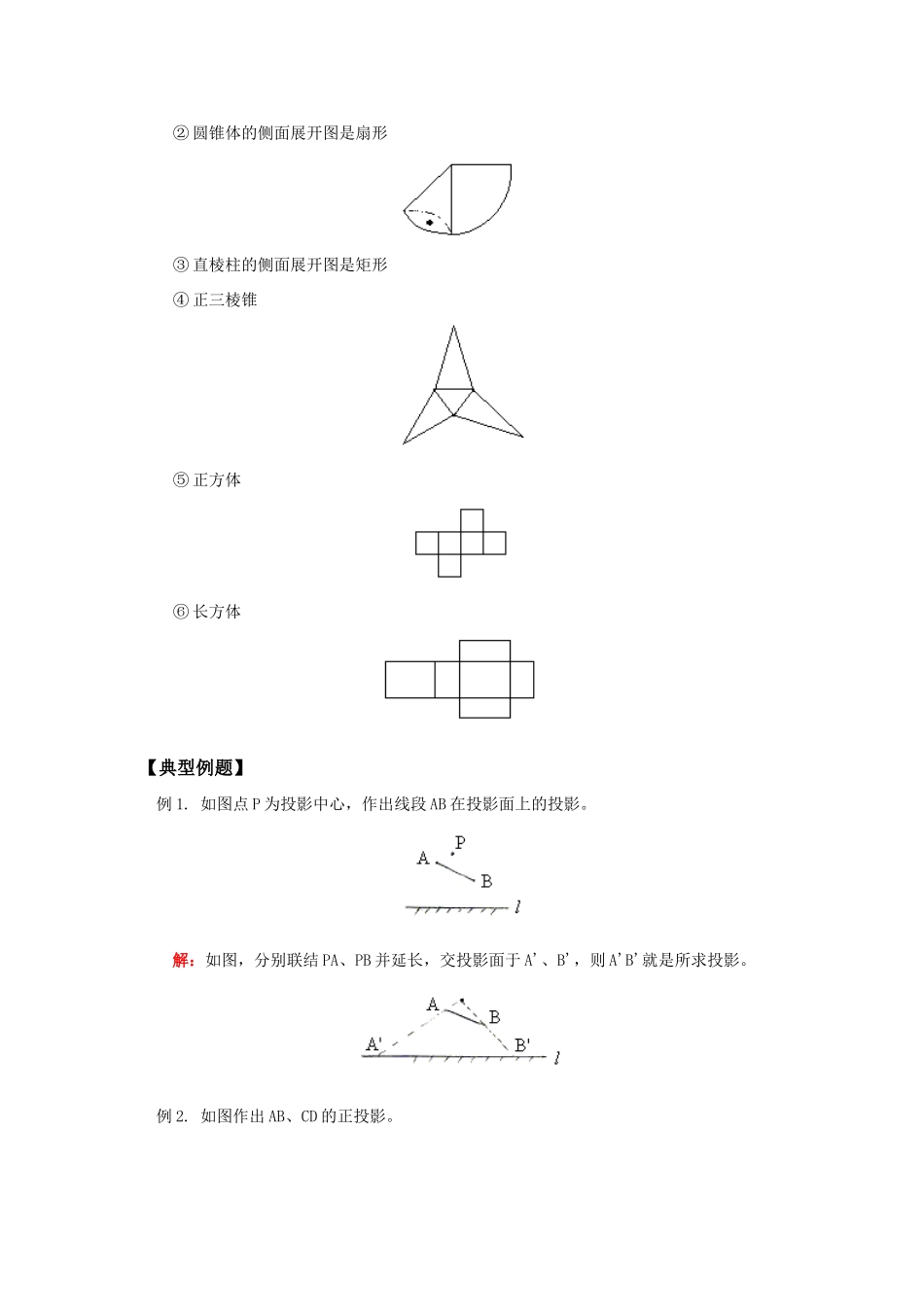
初三数学第二十六章投影、视图与展开图北京实验版【本讲教育信息】一.教学内容:第二十六章投影、视图与展开图二.教学目标:1.了解中心投影和平行投影的含义及其简单应用,知道物体的正投影与视图之间的关系。2.会画基本几何体的三视图,能根据三视图描述基本几何体或实物原型,实现基本几何体与三种视图之间的相互转化。3.了解直棱柱、圆柱、圆锥的平面展开图,能据展开图判断、制作简单的立体模型。4.进一步培养学生的动手操作和数学思维能力,发展学生的空间观念。三.教学重点、难点:(一)重点:通过所学知识,培养学生的空间观念和动手操作能力。(二)难点:学习过程中紧密联系实际,合理想象、培养空间观念。四.教学过程:(一)知识点:1.投影:物体在灯光或太阳光的照射下会产生影子,这种现象称作投影。2.中心投影:光线从一点发出的投影称为中心投影,这个点称为投影中心,光线称为投影线,投影所在的平面称为投影面。如图3.平行投影:在平行光线照射下形成的投影称为平行投影(如图2),在平行投影中如果投影线与投影面垂直,这种投影称为正投影(如图3)。4.中心投影与平行投影的区别:(1)中心投影的投影线交于一点,平行投影的投影线平行。(2)中心投影的形状不变,但大小会随着物体与投影中心的距离的变化而变化,当投影面与物体平行时,正投影不会改变物体的形状和大小。5.视图:物体的正投影称为视图,把从物体正面的视图称为主视图,从物体的左侧面得到的视图称为左视图,从物体上面得到的视图称为俯视图,统称三视图。6.三视图的位置:俯视图画在主视图的下方,左侧图画在主视图的右面。7.画三视图的“三等原则”:(1)主视图与俯视图的长度相等,且相互对正,即“长对正”(2)主视图与左视图的高度相等,且相互平齐,即“高平齐”(3)俯视图与左视图的宽度相等,即“宽相等”8.常见几何体的平面或侧面展开图①圆柱体的侧面展开图是矩形②圆锥体的侧面展开图是扇形③直棱柱的侧面展开图是矩形④正三棱锥⑤正方体⑥长方体【典型例题】例1.如图点P为投影中心,作出线段AB在投影面上的投影。解:如图,分别联结PA、PB并延长,交投影面于A'、B',则A'B'就是所求投影。例2.如图作出AB、CD的正投影。解:如图,分别作A、B、C、D点的投影点A'、B'、C'、D',联结A'B'、C'D',则A'B'、C'D'就是所求的正投影。例3.下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序排列正确的是()A.A→B→C→DB.D→B→C→AC.C→D→A→BD.A→C→B→D解:选C例4.三根垂直于地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图,试确定路灯灯泡的位置,再作出甲的影子。(不写作法,保留作图痕迹)解:A点为路灯灯泡的位置MN为甲的影子例5.画下面几何体的三视图解:例6.据下图所给的视图,说出它们所表示的几何体的名称。解:(1)表示几何体是圆台。(2)表示的几何体是正三棱锥。例7.观察下列图形,哪些可以围成正方体?哪些不能围成正方体?在此基础上进行总结。解:(1)(2)(3)(8)都可以组成正方体。总结:基本图形变式图形本章小结:【模拟试题】(答题时间:30分钟)一、填空题:1.三视图包括_________,_________,_________,从正面看,得到的视图是_________,从左面看,得到的视图是_________,从上往下看,得到的视图是_________。2.如图,是棱长为1cm的小正方体组成的几何体,那么,这个几何体的表面积是_________,主视图的面积是_________。3.一个圆柱的侧面展开图是相邻边长分别为10,16的矩形,则该圆柱的底面半径是_________。4.下图是一个物体的三视图,则该物体的形状是_________。二、选择题:1.如图,不是立方体表面展开图的是()2.对图1所示的几何体变换位置或视角,则可以得到的几何体是图2中的()图1图23.图3中几何体的主视图是图4中的()图3图44.如图,小明站在C处看甲、乙两楼楼顶上的A点和E点,点C、E、A在同一直线上,点B、D分别在点E、A的正下方,且D、B、C三点在同一直线上,B、C相距20米,D、C相距40米,乙楼高BE为15米,甲楼高AD为()米。(小明身高忽略不计)A.40B.20C.15D.30三、下图是由一些大小相同的小正方体组成的简...