安徽省合肥一中高三数学上学期第一次阶段考试试卷 文 新人教A版试卷VIP专享VIP免费

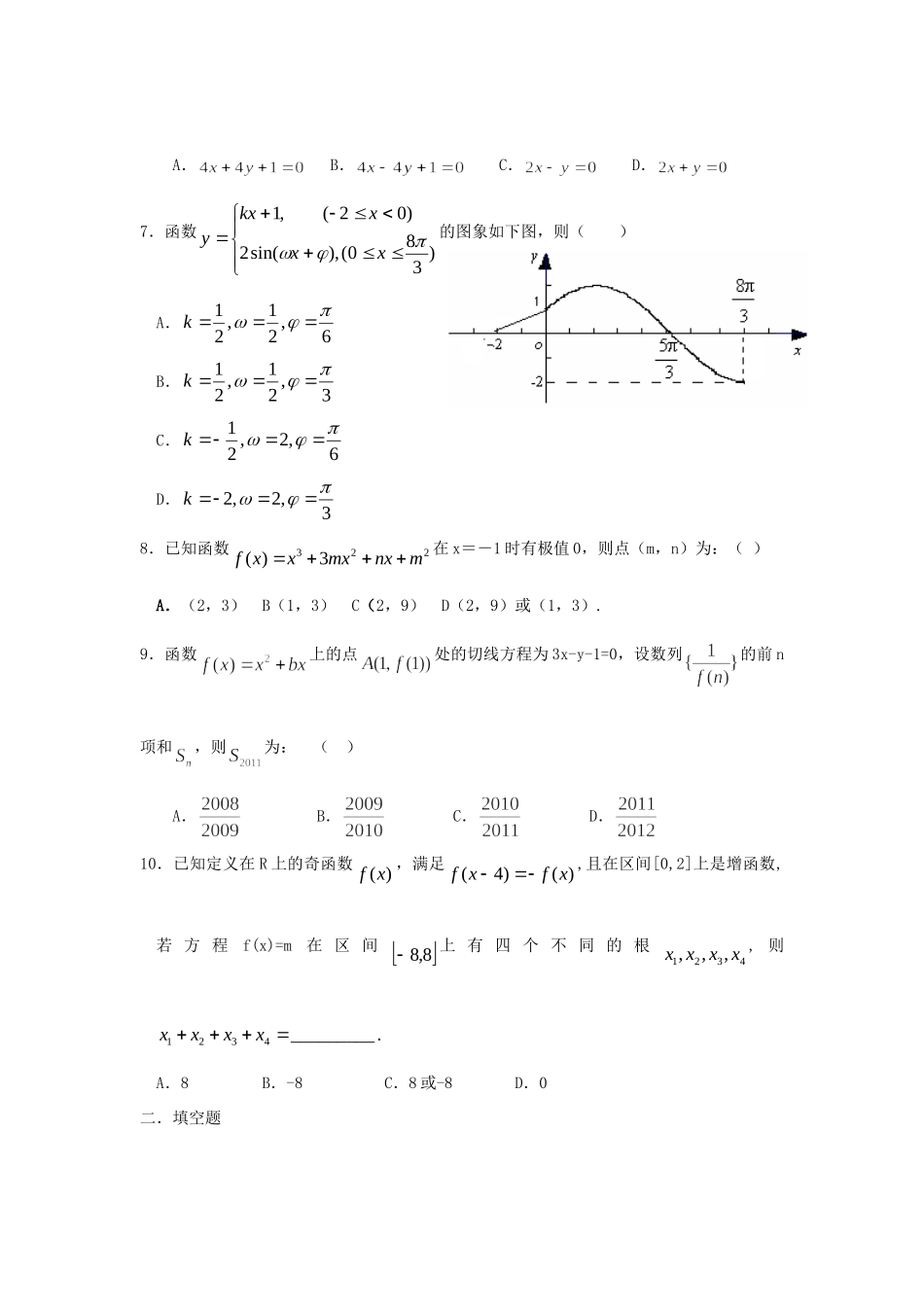
合肥一中2011~2012学年第一学期第一次阶段性考试高三数学（文）试卷一．选择题1．设全集U={1，2，3，4，5，7}，集合M={1，3，5，7}，集合N={3，5}，则（）A．B．C．D.2．已知是定义在R上的奇函数，且当时，，则=（）A．1B．C．-1D．3．设集合，集合，那么“”是“”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件4．已知是函数f(x)=2x+11x的一个零点.若1x∈（1，0x），2x∈（0x，+），则（）（A）f(1x)＜0，f(2x)＜0（B）f(1x)＜0，f(2x)＞0（C）f(1x)＞0，f(2x)＜0（D）f(1x)＞0，f(2x)＞05．为了得到函数sin(2)3yx的图像，只需把函数sin(2)6yx的图像（A）向左平移4个长度单位（B）向右平移4个长度单位（C）向左平移2个长度单位（D）向右平移2个长度单位6．若幂函数的图象经过点，则该函数在A点处的切线方程为（）A．B．C．D．7．函数)380(),sin(2)02(,1xxxkxy的图象如下图，则（）A．6,21,21kB．3,21,21kC．6,2,21kD．3,2,2k8．已知函数322()3fxxmxnxm在x＝－1时有极值0，则点（m，n）为：（）A．（2，3）B（1，3）C（2，9）D（2，9）或（1，3）.9．函数上的点处的切线方程为3x-y-1=0，设数列的前n项和，则为：（）A．B．C．D．10．已知定义在R上的奇函数)(xf，满足(4)()fxfx,且在区间[0,2]上是增函数,若方程f(x)=m在区间8,8上有四个不同的根1234,,,xxxx,则1234_________.xxxxA．8B．-8C．8或-8D．0二．填空题11．命题“存在，使得”的否定是12．已知），则.13．已知函数()'()cossin,4fxfxx则()4f的值为.14．已知，则不等式的解集_____15．已知函数xxf)21()(的图象与函数的图象关于直线xy对称，令|),|1()(xgxh则关于函数)(xh有下列命题:①)(xh的图象关于原点对称；②)(xh为偶函数；③)(xh的最小值为0；④)(xh在（0，1）上为减函数.其中正确命题的序号为（注：将所有正确命题的序号都填上）三．解答题16．已知函数()2sin()cosfxxx.（Ⅰ）求()fx的最小正周期；（Ⅱ）用五点法作图，作出函数在区间上的草图.17．已知函数32()3fxxaxx（I）若3x是()fx的极值点，求()fx在[1,]xa上的最小值和最大值；（Ⅱ）若()[1,)fxx在上是增函数，求实数a的取值范围。18．设函数2()sin()2cos1468xxfx．（Ⅰ）求函数()fx的单调递增区间．（Ⅱ）若函数()ygx与()yfx的图像关于直线1x对称，求当4[0,]3x时()ygx的最大值．19．在一个交通拥挤及事故易发生路段，为了确保交通安全，交通部门规定，在此路段内的车速v（单位：km/h）的平方和车身长l（单位：km）的乘积与车距d成正比，且最小车距不得少于半个车身长.假定车身长均为l（单位：km）且当车速为50（km/h）时，车距恰为车身长，问交通繁忙时，应规定怎样的车速，才能使在此路段的车流量Q最大？(车流量=车身长车距车速)20．在平面直角坐标中，已知三点A（-1，2），B（0，x+2）,共线，其中（1）将x表示为y的函数，并求出函数表达示y=f(x);（2）若y=f(x)在上是单调函数，求的取值范围；（3）若时，y=f(x)在上的最小值为，求的表达式。21．已知函数24(),0,2.33xfxxx(Ⅰ)求()fx的值域；(Ⅱ)设0a，函数321(),0,23gxaxaxx．若对任意10,2x，总存在00,2x，使10()()0fxgx，求实数a的取值范围．2011-2012年合肥一中高三第一次月考数学试卷文科答题卷一．选择题（共50分）题号12345678910选项二．填空题（共25分）11．12．13．14．15．三．解答题（共75分）16．17．18．19．20．21．