18.1勾股定理-(2)VIP免费

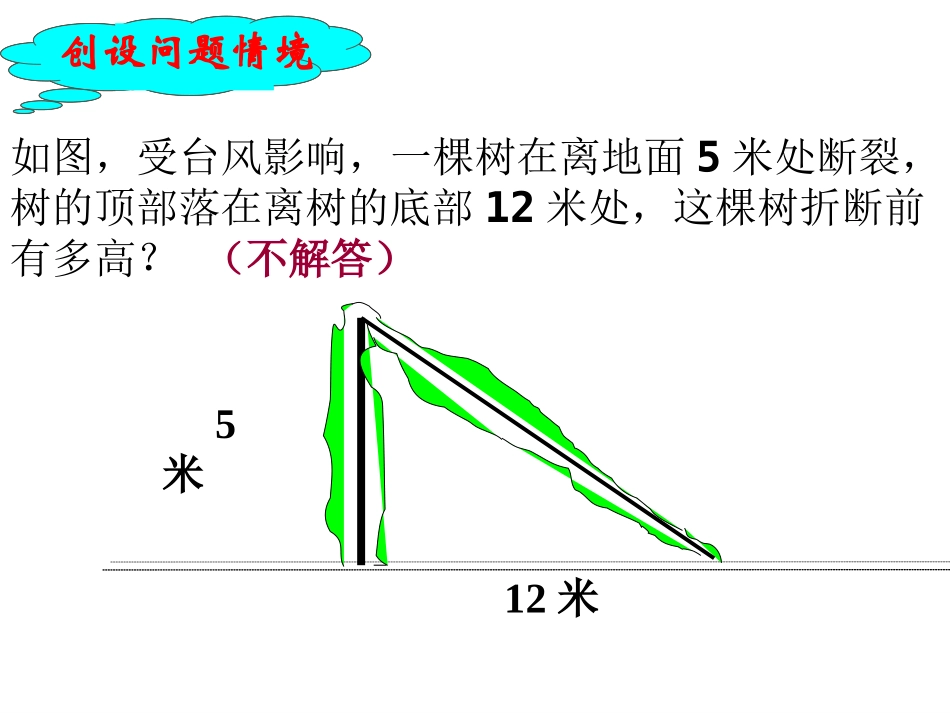
18.118.1勾股定理勾股定理沪科版八年级数学沪科版八年级数学（下册）（下册）田阳县民族中学黄美香如图，受台风影响，一棵树在离地面5米处断裂，树的顶部落在离树的底部12米处，这棵树折断前有多高？（不解答）y=0创设问题情境5米12米如图是一个行距、列距都是1的方格网，观察图中用彩色画出的三个正方形，谁能告诉我这三个正方形的面积S1、S2、S3之间有怎样的关系？用它们的边长表示，能得到怎样的式子？观察与思考：S2S1S3abc（图中每个小方格代表一个单位面积）ACBS1+S2=S3即：a2+b2=c2S2S1S3（图中每个小方格代表一个单位面积）图18-2S1+S2=S3，即：a2+b2=c2图18-3ABCabcACBS2S1S3观察左边图18-2、图18-3完成下表：图形S1S2S3关系图18-2图18-3991891625观察上表，你还能得到刚才的结论吗？S1+S2=S3S1+S2=S3abcS1=a2S2=b2S3=c2ABCabcS1S2S3S1+S2=S3其中，关系：猜想规律：a2+b2=c2故：直角三角形两条直角边的平方和，等于斜边的平方。文字表述：对于上述结论，要使人信服，必须加以证明。如何证明上述结论呢？问题情境已知：如图1，在RtABC△中，∠C=90°，AB=c,BC=a，AC=b.求证：.222cba图1aABCcb证明：取4个与RtABC△全等的直角三角形，把它们拼成边长为（a+b）的正方形。证明a、b、c之间的关系：a2+b2=c2aaaabbbbcccc证明a、b、c之间的关系：a2+b2=c2证明a、b、c之间的关系：a2+b2=c2aaaabbbbccccHGEFA1B1C1D1用面积法证明∴a2+b2+2ab＝c2+2ab∴a2+b2=c2a2+b2+2abc2+2ab证明a、b、c之间的关系：a2+b2=c2S正方形EFGH=4S直角三角形+S正方形A1B1C1D12214cab.22abc S正方形EFGH=(a+b)2=a2+b2+2abaaaabbbbccccHGEFA1B1C1D1从图中可见，A1B1=B1C1=C1D1=A1D1=c.因为∠B1A1E+A∠1B1E=90°,而∠A1B1E=D∠1A1H，因此∠B1A1E+D∠1A1H=90°,D∠1A1B1=90°.同理：∠A1B1C1=B∠1C1D1=C∠1D1A1=90°，所以四边形A1B1C1D1是边长为c的正方形。勾股定理如果直角三角形两直角边分别为a、b,斜边为c，那么：即：直角三角形两直角边的平方和等于斜边的平方。abc师生共识：.222cba勾股小知识勾股小知识早在三千多年前，周朝数学家商高就提出“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中，所以在我国人们就把这个定理叫作“商高定理”。商高定理就是勾股定理哦！勾股在中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.因此，我们称上述结论为勾股定理。毕达哥拉斯定理：毕达哥拉斯在国外，尤其在西方这个重要定理被称为“毕达哥拉斯定理”或“百牛定理”．相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现这个定理后异常高兴，命令他的学生宰了一百头牛来庆祝这个伟大的发现，因此又叫做“百牛定理”．勾股定理的作用就是知道直角三角形中任意两边就可以求出第三边。勾股定理的作用：比一比看看谁算得快！例：求下列直角三角形中未知边的长。运用勾股定理解题时，方程思想是常用的思想方法之一.方法小结:3x5810x125x=4=6=13勾股数1、常见勾股数有：3、4、5;5、12、13;7、24、25……2、如果a,b,c是一组勾股数，则ka、kb、kc（k为正整数）也是一组勾股数，如：6、8、10；9、12、15……3、一组勾股数中必有一个数是5的倍数勾股小知识勾股小知识例：如图，受台风影响，一棵树在离地面5米处断裂，树的顶部落在离树的底部12米处，这棵树折断前有多高？y=0应用知识回归生活(X－5)米解：设这棵树折断前有x米，222)5(125x即：.169)5(2x解这个方程，得：.8,1821xx故：。结合题意，不符合实际意义，应舍去，82x18x答：这棵树折断前有18米。5米12米如图，根据勾股定理得：迎接挑战迎接挑战1、已知直角三角形的两直角边边长分别为5,12，你能求第三边的长吗？迎接挑战迎接挑战2、已知直角三角形的两条边长分别为5,12，求第三边的长。解：设第三边的长为x。（1）当x为斜边时，有（2）当x为直角边时，有13125222xx，119512222xx，当第三边不确定是什么边时，要应用分类思想来解决...