1.1.1平均变化率VIP免费

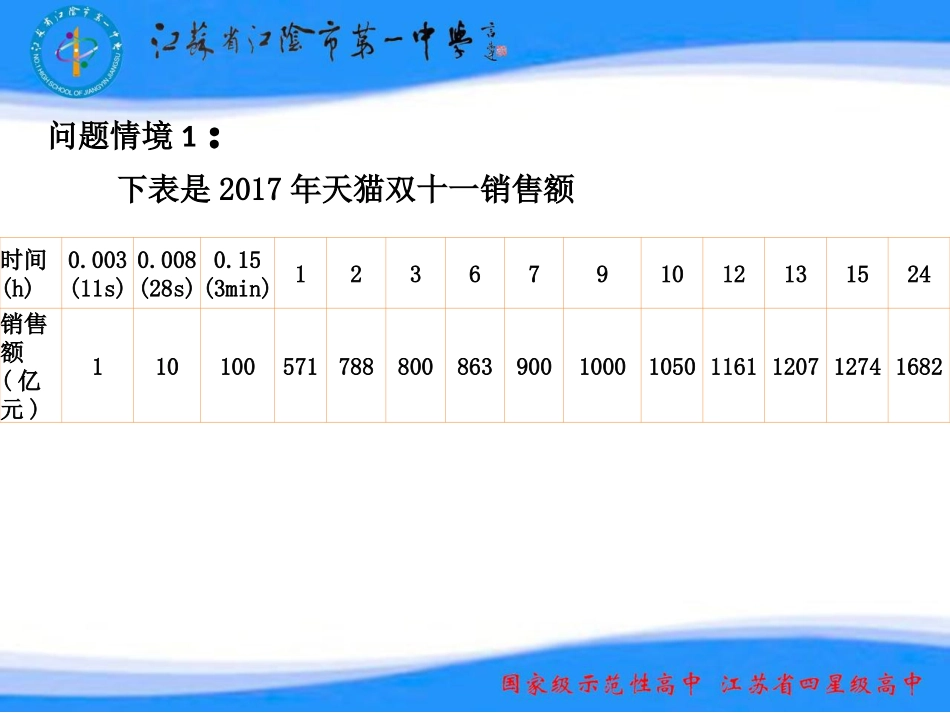
1.1.1平均变化率江阴市第一中学刘晔问题情境1：下表是2017年天猫双十一销售额时间(h)0.003(11s)0.008(28s)0.15(3min)1236791012131524销售额(亿元)110100571788800863900100010501161120712741682ABCDt/d2030342102030A(1,3.5)B(32,18.6)O210T/oC14.814.815.115.1C(34,33.4)问题2：从A到B的温差是多少？从B到C的温差是多少？问题3：从A到B这一段与从B到C这一段，你感觉哪一段的气温变化得较快？AB段气温上升得平缓，BC段气温则是陡然上升．问题1：你能说出A、B、C三点的坐标所表示意义吗？某市2017年3月18日到4月20日的日最高气温变化曲线:问题情境2：（注：3月18日为第一天）（3）曲线上BC之间的一段几乎成了直线，由此联想到如何量化直线的倾斜程度？CByy（1）的大小能否作为量化BC段陡峭的程度的量？CByyCBxx在考察的同时必须考察．学生活动学生活动（2）还必须考察什么量？案例中，从B到C气温“陡增”，这是我们从图像中的直观感觉，那么如何量化陡峭程度呢？t(d)20303422030ABOCT/oC210t/d2030342102030A(1,3.5)B(32,18.6)OC(34,33.4)T/oC21032346.184.33BCBCxxyy联想到用斜率来量化直线的倾斜程度，我们用比值：来近似地量化B,C之间这一段曲线的陡峭程度，并称该比值为气温在区间[32，34]上的平均变化率．2030342102030A(1,3.5)B(32,18.6)OC(34,33.4)T/oC210气温在区间[1，32]上的平均变化率为：气温在区间[32，34]上的平均变化率为：33.418.614.87.4(/)34322ms18.63.515.10.5(/)32131ms虽然点A，B之间的温差与点B，C之间的温差几乎相同，但它们的平均变化率却相差很大．t/d[问题4]如果将上述气温曲线看成是函数的图象，任取x1，x2[1，34]，则函数y=f(x)在区间[1，34]上的平均变化率为在区间[1，x1]上的平均变化率为在区间[x2，34]上的平均变化率为o1x234xyACy=f(x)x1f(x1)f(x2)f(1)f(34)1)1()(11xfxf2234)()34(xxff134)1()34(ff你能据此归纳出“函数的平均变化率”的一般性定义吗？f(34)-f(1)34-1xfyxf2121fxfxxxfx12,xx一般地，函数在区间上的平均变化率为曲线陡峭程度是平均变化率的“视觉化”．平均变化率是曲线陡峭程度的“数量化”，建构数学建构数学注意：不能脱注意：不能脱离区间而言离区间而言则平均变化率即为xyxxxfxf1212)()(xxfxxf)()(11若设，即将看作是对于的一个“增量”x1x2121fxfxxxfx12,xx一般地，函数在区间上的平均变化率为)()(1212xfxfyxxxOABxyy＝f(x)x1x2f(x1)f(x2)x2-x1=△xf(x2)-f(x1)=△y直线AB的斜率平均变化率xyxxxfxf1212)()(思考：思考：2121fxfxxxfx12,xx一般地，函数在区间上的平均变化率为的几何意义是什么？例1某婴儿从出生到第12个月的体重变化如图所示，试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率．t/月W/kg639123.56.58.611例题讲解例题讲解0t/月W/kg639123.56.58.611解：从出生到第3个月，婴儿体重平均变化率为从第6个月到第12个月，婴儿体重平均变化率为)月/(1035.35.6kg)月/(4.06126.811kg不同的区间上平均不同的区间上平均变化率可能不同变化率可能不同本题中两个不同平均变化率的实际意义是什么？0例2水经过虹吸管从容器甲中流向容器乙，ts后容器甲中水的体积（单位：），试计算第一个10s内V的平均变化率．ttV1.025)(3cm问题1例2中的平均变化率为负的实际意义是什么？解：在第一个10s内，体积V的平均变化率为103(10)(0)52520.25(/)100100cmsVV平均变化率平均变化率可正可负可为可正可负可为00问题2平均变化率可以为0吗？举例说明.甲甲乙乙例3已知函数分别计算在区间[-3，-1]，[0，5],[m,n]上及的平均变化率．,2)(,12)(xxgxxf)(xf)(xg你在解本题的过程中有没有发现什么？bkxy],[nm总结:一次函数在区间上的平均变化率等于斜率k.kxyxxxfxf1212)()(ABOxyy=f(x)x1x2f(x1)f(x2)△x△y你能解释为什么会出现这一现象吗？例4已知函数，分别计算在下列区间上的平均变化率：...