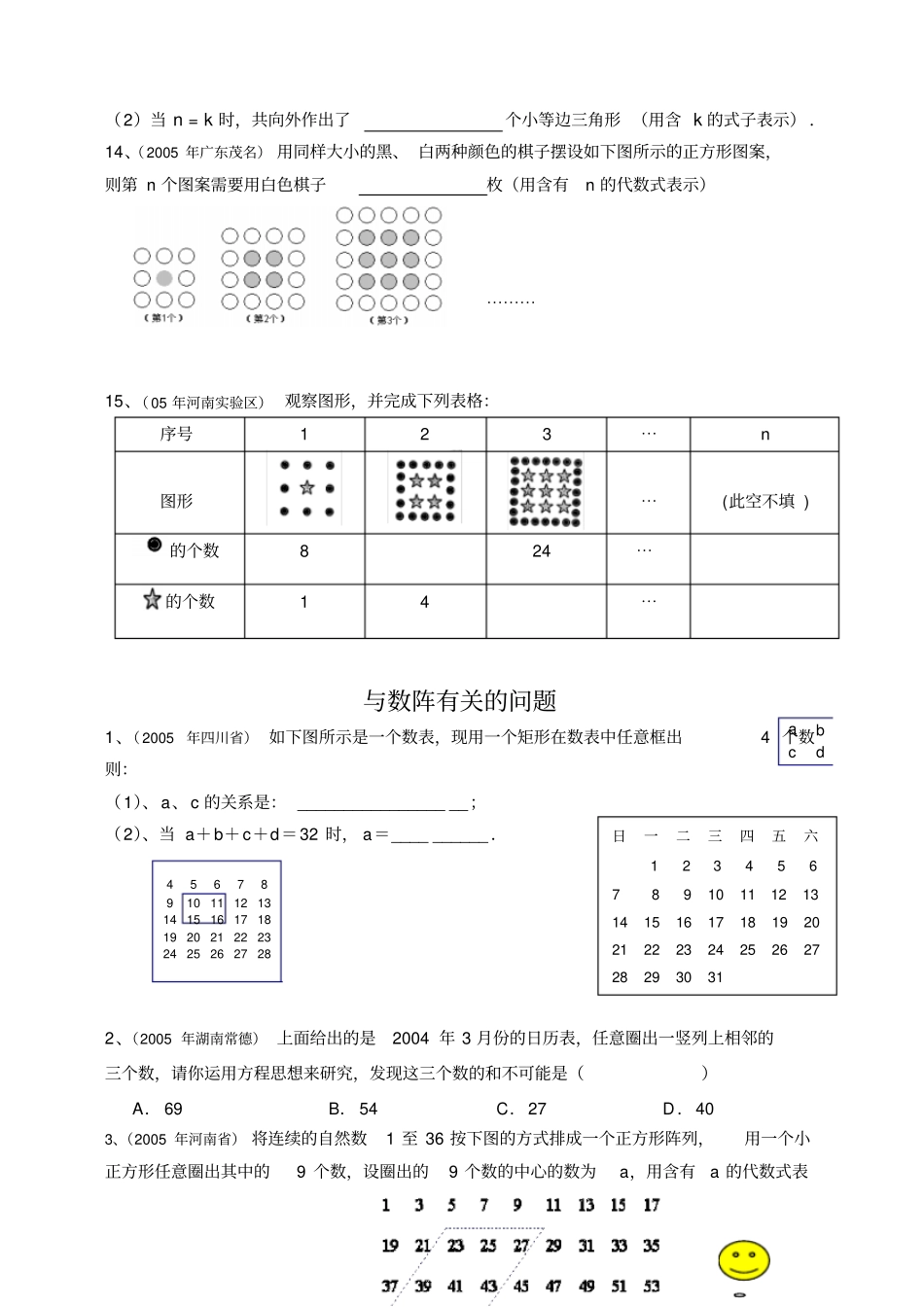
七年级数学(上)探索规律类问题班级学号姓名成绩一、数字规律类:1、一组按规律排列的数:41,93,167,2513,3621,⋯⋯请你推断第9个数是.2、(2005年山东日照)已知下列等式:①13=12;②13+23=32;③13+23+33=62;④13+23+33+43=102;⋯⋯⋯⋯由此规律知,第⑤个等式是.3、(2005年内蒙古乌兰察布)观察下列各式;①、12+1=1×2;②、22+2=2×3;③、32+3=3×4;⋯⋯⋯请把你猜想到的规律用自然数n表示出来。4、(2005年辽宁锦州)观察下面的几个算式:①、1+2+1=4;②、1+2+3+2+1=9;③、1+2+3+4+3+2+1=16;④、1+2+3+4+5+4+3+2+1=25,⋯⋯根据你所发现的规律,请你直接写出第n个式子5、(2005年江苏宿迁)观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、⋯,那么第2005个数是()A.1B.2C.3D.46、(2005年山东济南市)把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、⋯⋯,中间用虚线围的一列,从上至下依次为1、5、13、25、⋯⋯,则第10个数为________。第1行1第2行-23第3行-45-6第4行7-89-10第5行11-1213-1415⋯⋯⋯⋯⋯⋯7、(05年江苏省金湖实验区)已知一列数:1,―2,3,―4,5,―6,7,⋯将这列数排成如上所示的形式:按照上述规律排下去,那么第10行从左边数第5个数等于.二、图形规律类:1条2条3条图1图2图38、(2005年云南玉溪)一质点P从距原点1个单位的A点处向原点方向跳动,第一次跳动到OA的中点1A处,第二次从1A点跳动到O1A的中点2A处,第三次从2A点跳动到O2A的中点3A处,如此不断跳动下去,则第n次跳动后,该质点到原点O的距离为。9、(2005年江苏泰州)如下图是小明用火柴搭的1条、2条、3条“金鱼”⋯⋯,则搭n条“金鱼”需要火柴根.⋯⋯10、(05年广西玉林市)观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●⋯⋯⋯⋯从第1个球起到第2005个球止,共有实心球个.11、(2005年重庆市)如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,⋯⋯,则在第n个图形中,互不重叠的三角形共有个(用含n的代数式表示)。12、(2005年宁夏回族自治区)“◆”代表甲种植物,“★”代表乙种植物,为美化环境,采用如图所示方案种植.按此规律第六个图案中应种植乙种植物_________株.★★★★★★★◆◆◆★★◆◆★★★★◆★★★◆◆◆★★◆◆★★★★图1★★★◆◆◆图2★★★★图313、(2005年江苏南通市)已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示).(1)当n=5时,共向外作出了个小等边三角形n=3n=4n=5(第13题)⋯⋯dcba45678910111213141516171819202122232425262728(2)当n=k时,共向外作出了个小等边三角形(用含k的式子表示).14、(2005年广东茂名)用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子枚(用含有n的代数式表示)⋯⋯⋯15、(05年河南实验区)观察图形,并完成下列表格:序号123⋯n图形⋯(此空不填)的个数824⋯的个数14⋯与数阵有关的问题1、(2005年四川省)如下图所示是一个数表,现用一个矩形在数表中任意框出4个数则:(1)、a、c的关系是:__________________;(2)、当a+b+c+d=32时,a=__________.2、(2005年湖南常德)上面给出的是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是()A.69B.54C.27D.403、(2005年河南省)将连续的自然数1至36按下图的方式排成一个正方形阵列,用一个小正方形任意圈出其中的9个数,设圈出的9个数的中心的数为a,用含有a的代数式表日一二三四五六12345678910111213141516171819202122232425262728293031示这9个数的和为。4、(2005恩施自治州)下图的数阵是由全体奇数排成(1)图中平行四边形框内的九个数之和与中间的数有什么关系?(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种...