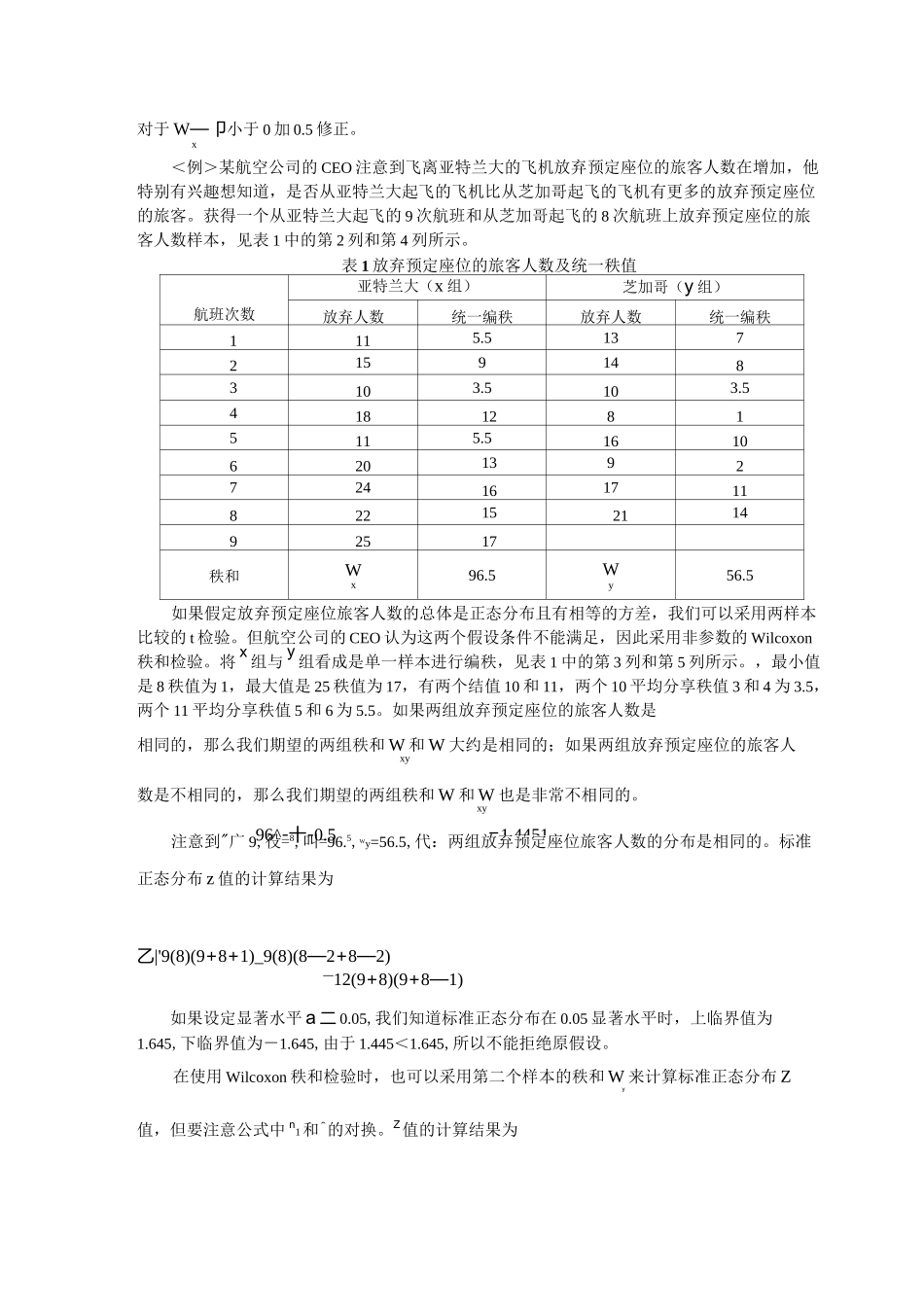
12(1)(2)我们定Wilcoxon秩和检验Wilcoxon符号秩检验是由威尔科克森(F・Wilcoxon)于1945年提出的。该方法是在成对观测数据的符号检验基础上发展起来的,比传统的单独用正负号的检验更加有效。1947年,Mann和Whitney对Wilcoxon秩和检验进行补充,得到Wilcoxon-Mann-Whitney检验,由后续的Mann-Whitney检验又继而得到Mann-Whitney-U检验。一、两样本的Wilcoxon秩和检验由Mann,Whitney和Wilcoxon三人共同设计的一种检验,有时也称为Wilcoxon秩和检验,用来决定两个独立样本是否来自相同的或相等的总体。如果这两个独立样本来自正态分布和具有相同方差时,我们可以采用t检验比较均值。但当这两个条件都不能确定时,我们常替换t检验法为Wilcoxon秩和检验。Wilcoxon秩和检验是基于样本数据秩和。先将两样本看成是单一样本(混合样本)然后由小到大排列观察值统一编秩。如果原假设两个独立样本来自相同的总体为真,那么秩将大约均匀分布在两个样本中,即小的、中等的、大的秩值应该大约均匀被分在两个样本中。如果备选假设两个独立样本来自不相同的总体为真,那么其中一个样本将会有更多的小秩值,这样就会得到一个较小的秩和;另一个样本将会有更多的大秩值,因此就会得到一个较大的秩和。设两个独立样本为:第一个x的样本容量为ni,第二个y样本容量为役,在容量为n二n+n的混合样本(第一个和第二个)中,,样本的秩和为W,y样本的秩和为W,y且有W+W=1+2+…+n=n(n+Dxy2W=W-ni(ni+1)1x2n(n+1)…以x样本为例,若它们在混合样本中享有最小的n个秩,于是W=宀,也是W可1x2xn(n+1)…能取的最小值;同样W可能取的最小值为。那么,W的最大取值等于混合样本y2x(7)(4(5如果样本中存在nno2=12将影响到公式(28.5)中的方差,按结值调整方差的公式为(n+n+1)nn工(T3—T)12—1_2jj(6其中T第j个结值的个数。j结值的存在将使原方差变小,这是一个显然正确的事实。标准W—u土0.5z———W-n1W+n+1)土0.5x~N(0,1n(n+1)n(n+1)的总秩和减去W的最小值,即-亠2;同样,W的最大取值等于y22yn(n+1)n(n+1)2—亠电。所以,⑵和⑶式中的气和W2均为取值在0与n(n+1)n(n+1)n(n+1)-亠+—〜—nn的变量。当原假设为真时,所有的x和y相当于从22212ii同一总体中抽得的独立随机样本,x和y构成可分辨的排列情况,可看成一排n个球随机地ii扌旨定n个为x球另n2个为y球,共有Cn种可能,而且它们是等可能的。基于这样分析,在原假设为真的条件下不难求出气和W2的概率分布,显然它们的分布还是相同的,这个分布称为样本大小为n1和n2的Mann-Whitney-Wilcoxon分布。一个具有实际价值的方法是,对于每个样本中的观察数大于等于8的大样本来说,我们nn可以采用标准正态分布z来近似检验。由于W]的中心点为号,根据(28.2)式,W中心点nnn(n+1)n(n+n+1)u=12+1——11——12_22W的方差o2从数学上可推导出xnn(n+n+1)o2—1212—12,nn(n+n+1),1212—1212(n+n)(n+n—1)1212其中分子加0.5或减0.5是为了对离散变量进行连续性修正,对于W-卩大于0减0.5修正,x96^-十-0.5=1.4451对于W—卩小于0加0.5修正。x<例>某航空公司的CEO注意到飞离亚特兰大的飞机放弃预定座位的旅客人数在增加,他特别有兴趣想知道,是否从亚特兰大起飞的飞机比从芝加哥起飞的飞机有更多的放弃预定座位的旅客。获得一个从亚特兰大起飞的9次航班和从芝加哥起飞的8次航班上放弃预定座位的旅客人数样本,见表1中的第2列和第4列所示。表1放弃预定座位的旅客人数及统一秩值航班次数亚特兰大(x组)芝加哥(y组)放弃人数统一编秩放弃人数统一编秩1115.513721591483103.5103.541812815115.51610620139272416171182215211492517秩和Wx96.5Wy56.5如果假定放弃预定座位旅客人数的总体是正态分布且有相等的方差,我们可以采用两样本比较的t检验。但航空公司的CEO认为这两个假设条件不能满足,因此采用非参数的Wilcoxon秩和检验。将x组与y组看成是单一样本进行编秩,见表1中的第3列和第5列所示。,最小值是8秩值为1,最大值是25秩值为17,有两个结值10和11,两个10平均分享秩值3和4为3.5,两个11平均分享秩值5和6为5.5。如果两组放弃预定座位的旅客人数是相同的,那么我们期望的两组秩和W和W大约是相同的...