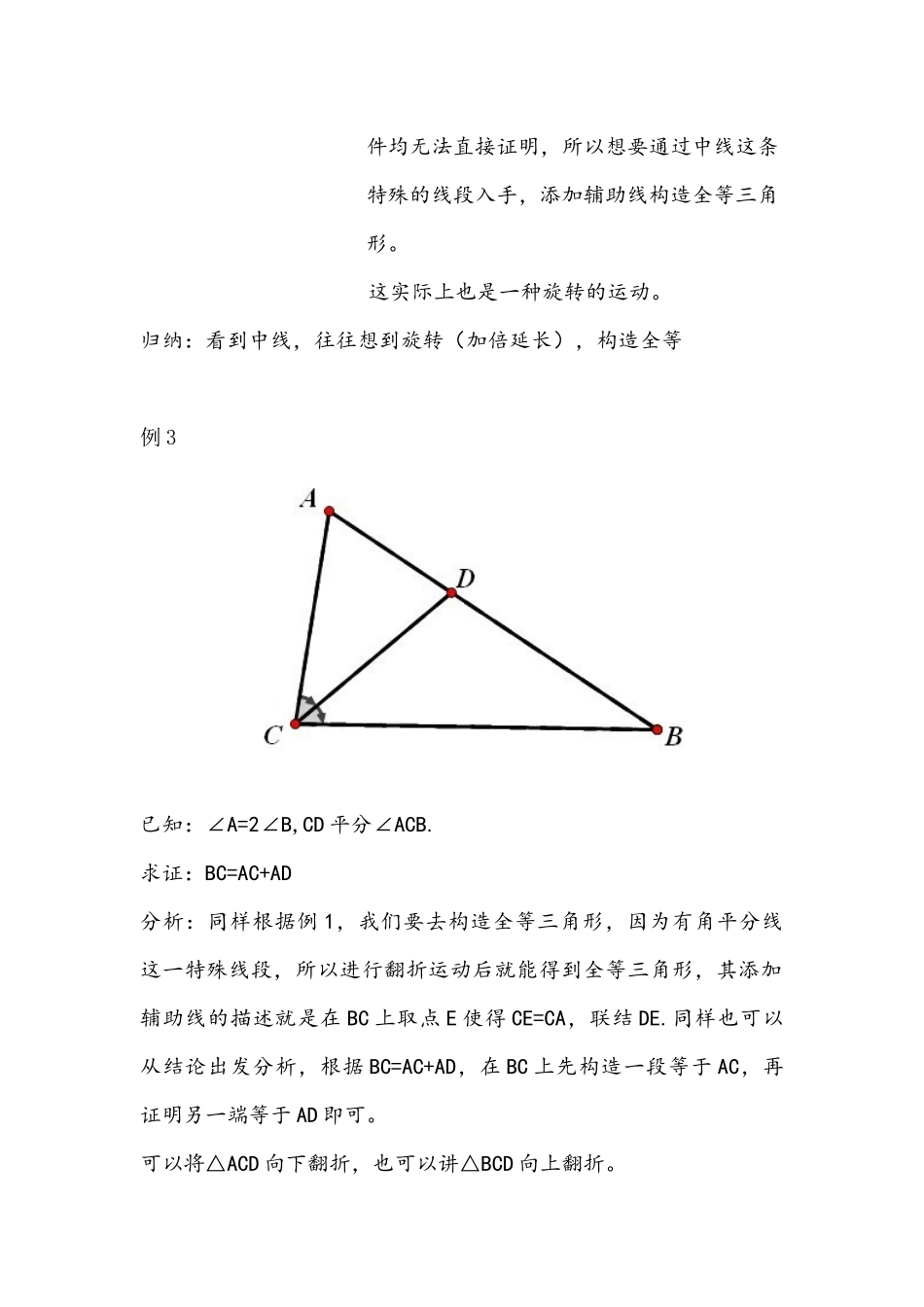
数学技能的习得:辅助线添法——“倍长中线”和“截长补短”在初中数学学习的过程中,学生们对于如何添加辅助线有一定的难度,如何习得这一数学技能,如何使学生了解添加辅助线的原因,如何掌握几种常用添加辅助线的方法便成了影响学生学业成绩的重要因素。使得学生学会分析如何添加辅助线。笔者在此基础上,设计下列教学案例,想要让学生学会利用倍长中线和截长补短的方法解决几何证明辅助线的添法。(一)课前提问:在解决几何问题中,为什么要添加辅助线?在添加辅助线的过程中,有哪些要注意的地方?(二)新课例题:例1:已知:四边形ABCD中,AB=CD,∠B=∠C求证:∠A=∠D.提问:证明角相等的方法有哪些?分析:分别从条件和结论两方面入手分析,从条件入手,则添加辅助线构造等腰三角形,从结论入手,则添加辅助线构造权等三角形。归纳:添加辅助线的方法:1.构造等腰三角形;2.构造全等三角形.例2:已知:△ABC中,D是BC上一点,BD=CD,∠1=∠2求证:AB=AC.提问:证明线段相等的方法有哪些?分析:由例题1,我们希望去构造全等或等腰,可是目前图形与条件均无法直接证明,所以想要通过中线这条特殊的线段入手,添加辅助线构造全等三角形。这实际上也是一种旋转的运动。归纳:看到中线,往往想到旋转(加倍延长),构造全等例3已知:∠A=2∠B,CD平分∠ACB.求证:BC=AC+AD分析:同样根据例1,我们要去构造全等三角形,因为有角平分线这一特殊线段,所以进行翻折运动后就能得到全等三角形,其添加辅助线的描述就是在BC上取点E使得CE=CA,联结DE.同样也可以从结论出发分析,根据BC=AC+AD,在BC上先构造一段等于AC,再证明另一端等于AD即可。可以将△ACD向下翻折,也可以讲△BCD向上翻折。归纳:看到角平分线,往往想到翻折(截长补短),构造全等例4:已知:△ABC中,AD是BC边上的高,AB+BD=DC求证:∠B=2∠C.让学生自行思考如何添加辅助线.归纳:看到高,往往想到翻折(截长补短),构造全等.练习:已知:在△ABC中,AB=2AC,D为AB的中点,E为AD的中点.求证:BC=2CE.通过以上的教学,笔者帮助学生概括了辅助线的构造方法:1.构造全等三角形;2.构造等腰三角形。讲解了如何添加辅助线的策略:1.看到中线,往往想到旋转(加倍延长),构造全等;2.看到角平分线,往往想到翻折(截长补短),构造全等;3.看到高,往往想到翻折(截长补短),构造全等。学生在此基础上,证明题的正确率得到了较大的提高。