勾股定理在生活中的应用VIP免费

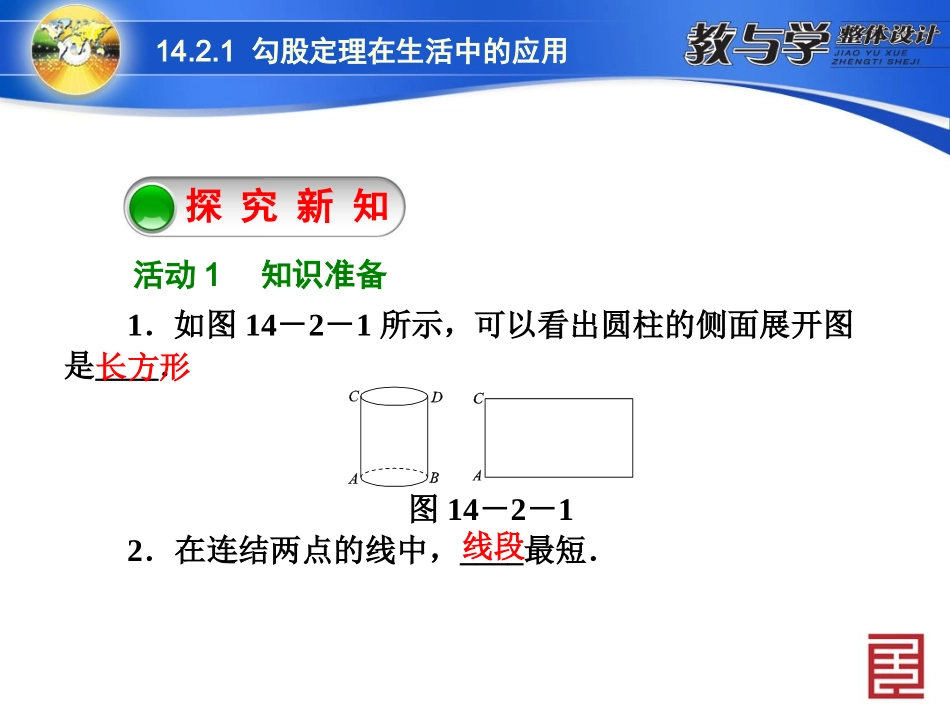
数学新课标（HS）八年级上册新知梳理新知梳理重难互动探究重难互动探究探究新知探究新知14.2.1勾股定理在生活中的应用14.2.1勾股定理在生活中的应用探究新知活动1知识准备1．如图14－2－1所示，可以看出圆柱的侧面展开图是____．图14－2－12．在连结两点的线中，____最短．线段长方形14.2.1勾股定理在生活中的应用活动2教材导学生活中勾股定理的应用一个圆柱，将其侧面剪开，展开成一个长方形，如图14－2－2①所示．沿着圆柱中心面剖开，截面也是一个长方形，如图②所示．设该圆柱的半径为r，高为h，回答下列问题．图14－2－214.2.1勾股定理在生活中的应用(1)用一根铁丝缠绕连结A，B两点，计算铁丝最短长度，用图①计算，应用等式为____．(2)点A到点B的直线距离可用图②计算，应用等式为____．(3)题(1)中如果是A，C′两点，计算铁丝最短长度，用图①计算，应用等式为____．◆知识链接——[新知梳理]知识点三AC′2＝(2πr)2＋h2AB2＝(πr)2＋h2AB2＝(2r)2＋h2实际问题转化为数学问题后，利用题中的直角三角形信息，直接应用勾股定理求解．实际问题转化为数学问题后，不能直接求出线段的长，则应根据题中与直角三角形有关的信息，考虑添加辅助线，构造直角三角形进行求解．新知梳理14.2.1勾股定理在生活中的应用►知识点一直接应用型►知识点用拼图的方法说明勾股定理求几何体表面两点之间的最短距离，通常将几何体的表面展开，把立体图形转化为____，再根据“两点之间，线段最短”这个公理找到最短距离，然后利用勾股定理进行计算求解．►知识点三最短路线型平面图形重难互动探究14.2.1勾股定理在生活中的应用探究问题一图形表面的最短路径问题如图14－2－3所示，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处(三条棱长如图14－2－3所示)，问怎样走路线最短？最短路线长为多少？图14－2－314.2.1勾股定理在生活中的应用[解析]蚂蚁由A点沿长方体的表面爬行到C1点，有三种方式，分别展成平面图形如图14－2－4：图14－2－414.2.1勾股定理在生活中的应用解：如图14－2－4①，在Rt△ABC1中，AC21＝AB2＋BC21＝42＋32＝25，∴AC1＝25.如图②，在Rt△ACC1中，AC21＝AC2＋CC21＝62＋12＝37，∴AC1＝37.如图③，在Rt△AB1C1中，AC21＝AB21＋B1C21＝52＋22＝29，∴AC1＝29.∵25＜29＜37，∴沿图①的方式爬行路线长最短，最短的路线长为5.14.2.1勾股定理在生活中的应用[归纳总结]解决有关立体图形中路线最短的问题，其关键是把几何体上的路线问题转化为平面上的路线问题．如圆柱侧面展开为长方形，圆锥侧面展开为扇形，长方体的侧面沿某一条棱展开为长方形等．运用平面上两点之间线段最短的道理，利用勾股定理求解．14.2.1勾股定理在生活中的应用例2如图14－2－5，是飞船舱内一个长、宽、高分别为50cm，40cm，30cm的长方体的空间，宇航员能否把一根长为70cm的实验仪器放进去？请说明你的理由．图14－2－5解：在直角三角形ABC中，因为∠ABC＝90°，AB＝50Cm，BC＝40Cm，所以AC2＝AB2＋BC2＝502＋402＝2500＋1600＝4100;在直角三角形A1AC中，∠A1AC＝90°，AC2＝4100，A1A2＝302，所以A1C2＝A1A2＋AC2＝302＋4100＝5000.所以长方体内最长对角线A1C的长的平方为5000＞4900＝702.故仪器能放进去．14.2.1勾股定理在生活中的应用[归纳总结]解有关勾股定理的实际应用问题的关键是将实际问题转化为数学模型，利用勾股定理，列方程求解.由于勾股定理反映的是直角三角形三边之间的关系，常常与方程“联姻”，这一点应尤其注意．