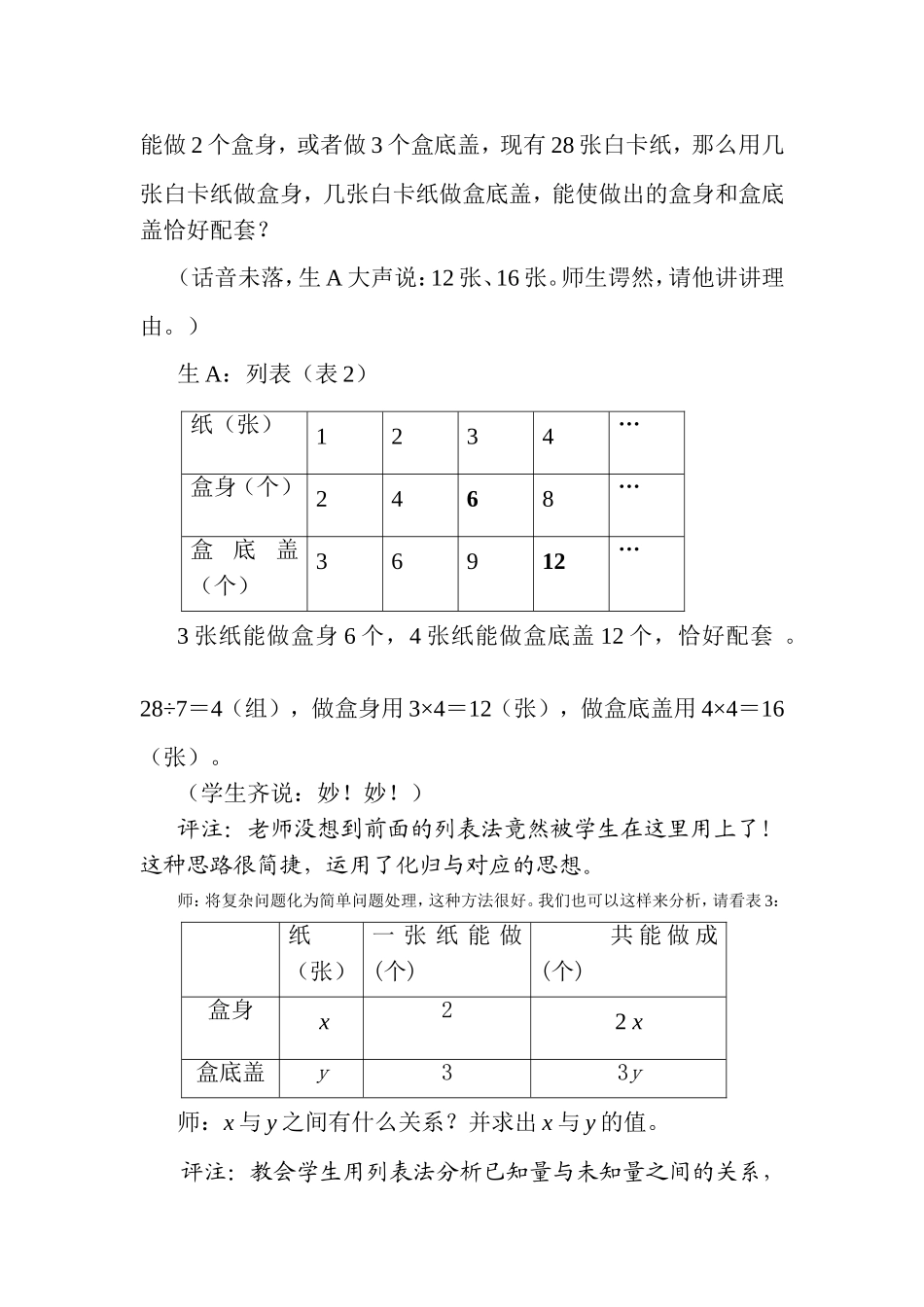
《实践与探索》一节课的实录与思考徐州市教育局教研室陈大勇一、背景介绍我市市区于2003年秋进入课改实验,使用的是华师大版数学教材。这学期在听课中发现有些教师把《实践与探索》等同于传统应用题来讲解,为了探讨《实践与探索》的教学方法,我在矿大附中上了一节课,课题是《第七章“实践与探索”问题1》。教学设备有实物投影仪。二、案例描述1、低起点引入问题。(老师拿出一个纸盒,展示它的两个底盖、一个盒身。)师:1个盒身配2个盒底盖能做一个盒子,请一起填表1:盒身(个)1234…ax盒底盖(个)2468…2ay师:x与y之间有什么关系?(学生议论:x=2y,y=2x,。教师板书,学生相互说理,判断对错。)评注:教学起点低,通过具体数字过渡到字母,渗透换元思想,让学生自己理解盒身与盒底盖数量之间的对应关系。大字表师:一个盒身配2个盒底盖能做一个包装盒,如果一张白卡纸能做2个盒身,或者做3个盒底盖,现有28张白卡纸,那么用几张白卡纸做盒身,几张白卡纸做盒底盖,能使做出的盒身和盒底盖恰好配套?(话音未落,生A大声说:12张、16张。师生谔然,请他讲讲理由。)生A:列表(表2)纸(张)1234…盒身(个)2468…盒底盖(个)36912…3张纸能做盒身6个,4张纸能做盒底盖12个,恰好配套。28÷7=4(组),做盒身用3×4=12(张),做盒底盖用4×4=16(张)。(学生齐说:妙!妙!)评注:老师没想到前面的列表法竟然被学生在这里用上了!这种思路很简捷,运用了化归与对应的思想。师:将复杂问题化为简单问题处理,这种方法很好。我们也可以这样来分析,请看表3:纸(张)一张纸能做(个)共能做成(个)盒身x22x盒底盖y33y师:x与y之间有什么关系?并求出x与y的值。评注:教会学生用列表法分析已知量与未知量之间的关系,帮助学生找出等量关系。(老师在巡视中发现有两种方法,分别请两位学生板演。)生B:(方法一)设用x张做盒身,y张做盒底盖。则解之得答:略。生C:(方法二)设做了盒身x个,盒底盖y个。则解之得24÷2=12(张),48÷3=16(张)。答:略。评注:问题(2)是整数解,学生易理解。不要求全体学生都能掌握两种解法,通过解决问题的过程,理解了一种解法,能用数学语言完整的表达解决问题的过程,就达到基本目标。二、自主探索解决问题师:请同学们看课本第35页的问题1,先自己做一做,然后再讨论。问题1:用20张白卡纸做包装盒,每张白卡纸能做盒身2个,或者盒底盖3个。1个盒身和2个盒底盖可以做成一个包装盒。那么能否把这些白卡纸分成两部分,一部分做盒身,一部分做盒底盖,正好配套?(学生在做的过程中,议论“是不是题目错了,怎么解出来的是分数”,老师没有直接回答,让学生自己讨论,同时分别请两组同伴上黑板合作完成。)生D与C合作:(方法一)设用x张纸做盒身,y张纸做盒底盖。则解之得盒身:8×2=16(个),盒底盖:11×3=33(个),所以能做16个包装盒,将剩下的一张纸再做一个盒身和一个盒底,就有17个身,34个底,可做17个包装盒。生E与F合作:(方法二)设做了x个盒身,y个盒底盖。则解之得17个盒身和34个盒底盖恰好配套,所以能做17个包装盒。师:请同学们对黑板上的两种做法给予评论。(多数同学赞同第一种方法,认为第二种方法没有说清各用几张纸做盒身和盒底盖。)生E补充:17÷2=8,34÷3=11,所以用8张纸做16个盒身用11张纸做33个盒底盖,最后一张纸做1个盒身和1个盒底盖。评注:问题1是开放的,解决时有一定难度,采用2位同学上黑板做同一题,是为了能合作交流、相互纠正补充。教师在巡视时,没有简单地对“做16个盒”的学生说“错”,对“做17个盒”的学生说“对”,而是鼓励学生要说的有道理。通过合作交流,让学生体会到解决实际问题的多样性,培养分类讨论、合情推理的思想。学生A又一次站起来说:同学们做的都对,但我们还是用列表法:从表2中看出用7张纸能做6个盒子,用14张纸能做12个盒子。在余下的6张纸里,用2张纸做4个盒身、3张纸做9个盒底盖,最后1张纸做1个盒身和1个盒底盖,这样能再做5个盒子,所以可做17个盒子。(同学又纷纷叫“好!”)评注:“对应、分组”的思维模式一直是这位同学的主导思想,应该...