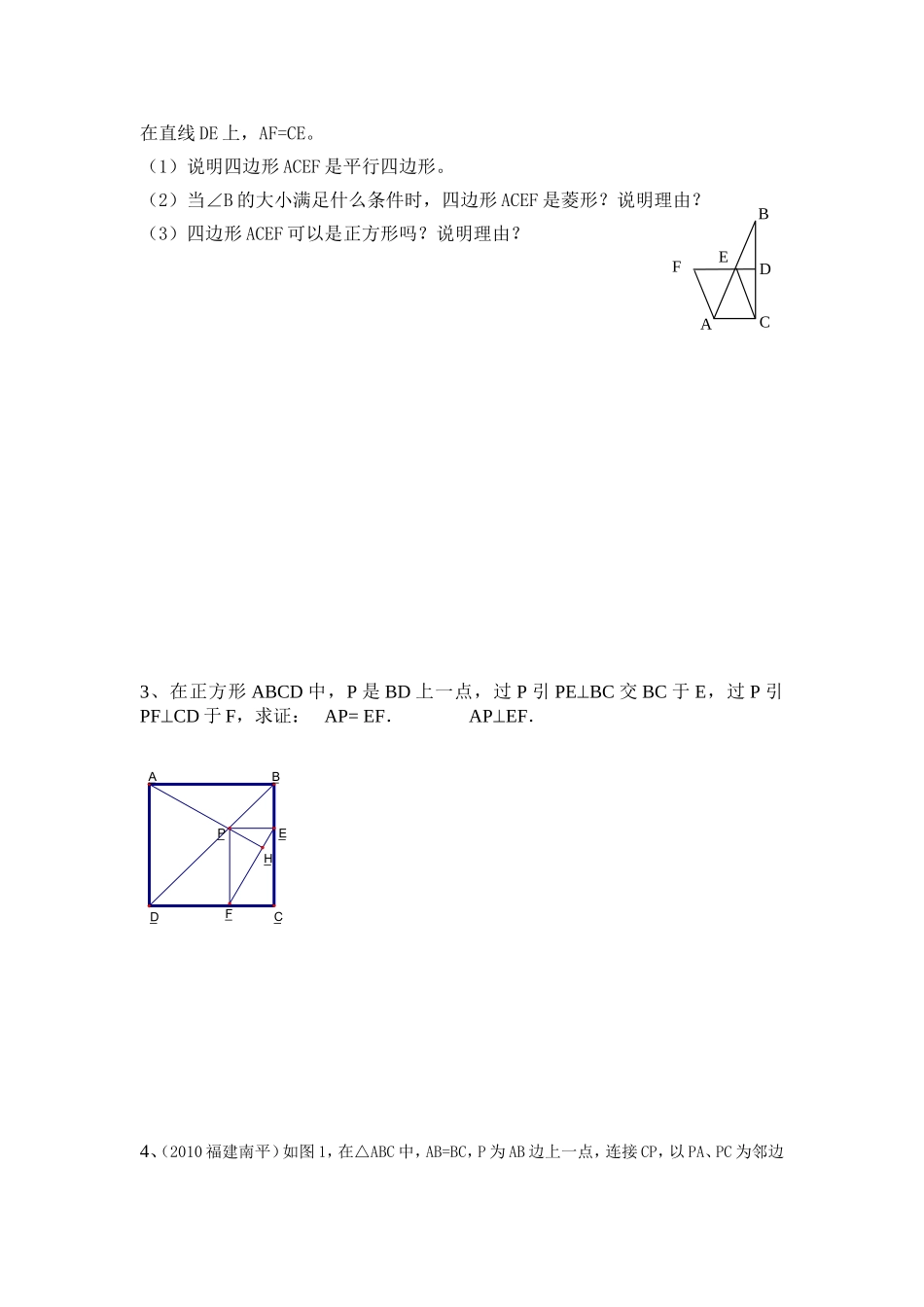
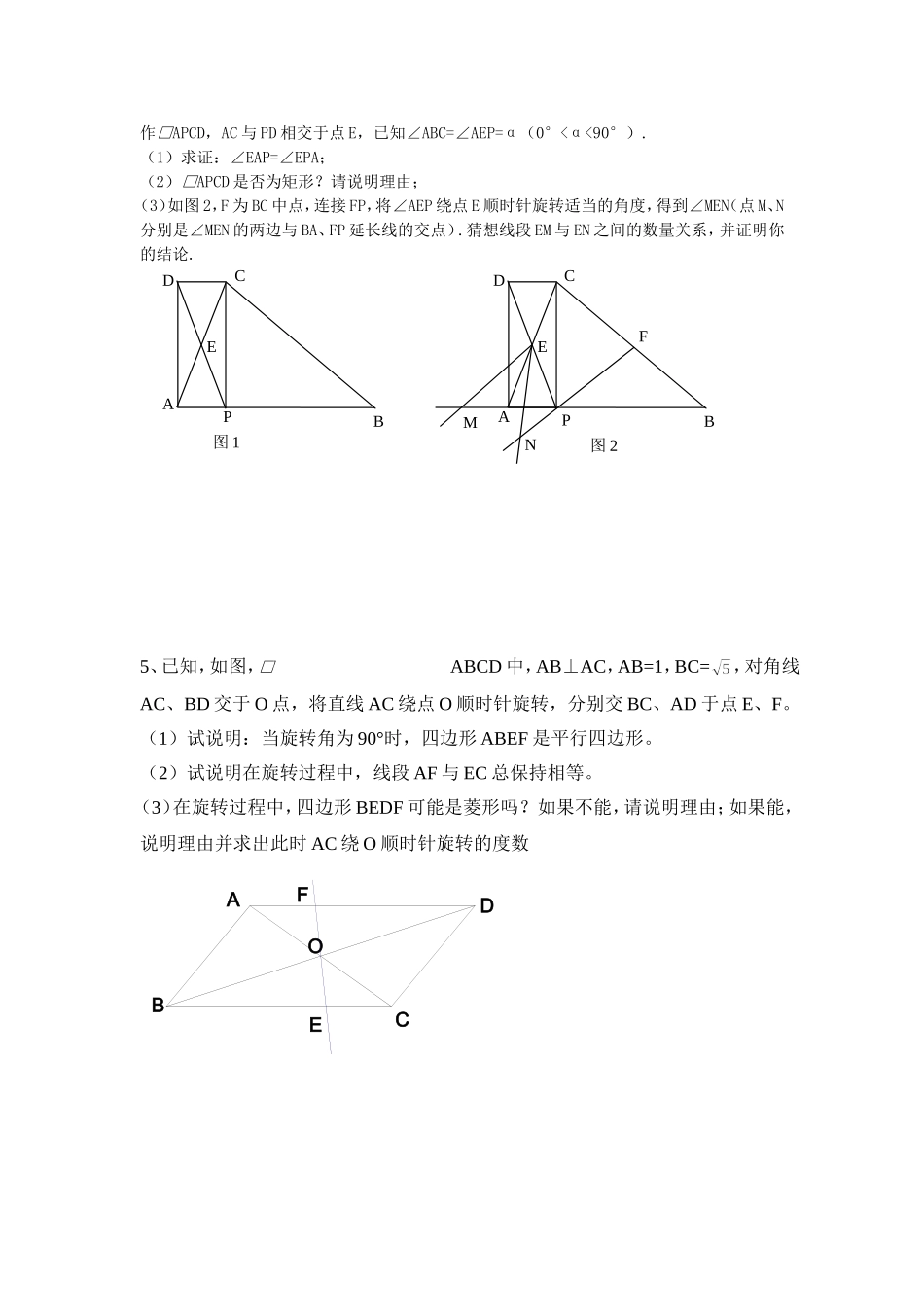
1:如图:□ABCD中,AB=2cm,BC=12cm,∠B=45,点P在边BC上,由点B向点C运动,速度为每秒2cm,点Q在边AD上,由点D向点A运动,速度为每秒1cm,连接PQ,设运动时间为秒.(1)当为何值时,四边形ABPQ为平行四边形;(2)设四边形ABPQ的面积为,请用含有t的代数式表示的值;(3)当P运动至何处时,四边形ABPQ的面积是口ABCD面积的四分之三?2、如图在△ABC中,∠ACB=90°,BC垂直平分线DE交BC于D,交AB于点E,点F在直线DE上,AF=CE。(1)说明四边形ACEF是平行四边形。(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?说明理由?(3)四边形ACEF可以是正方形吗?说明理由?3、在正方形ABCD中,P是BD上一点,过P引PEBC交BC于E,过P引PFCD于F,求证:AP=EF.APEF.4、(2010福建南平)如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边_C_B_A_D_F_P_E_HACDBEF作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).(1)求证:∠EAP=∠EPA;(2)□APCD是否为矩形?请说明理由;(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.5、已知,如图,□ABCD中,AB⊥AC,AB=1,BC=,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点E、F。(1)试说明:当旋转角为90°时,四边形ABEF是平行四边形。(2)试说明在旋转过程中,线段AF与EC总保持相等。(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕O顺时针旋转的度数OBFADCE图1ABDCEP图2ABDCEPMNF