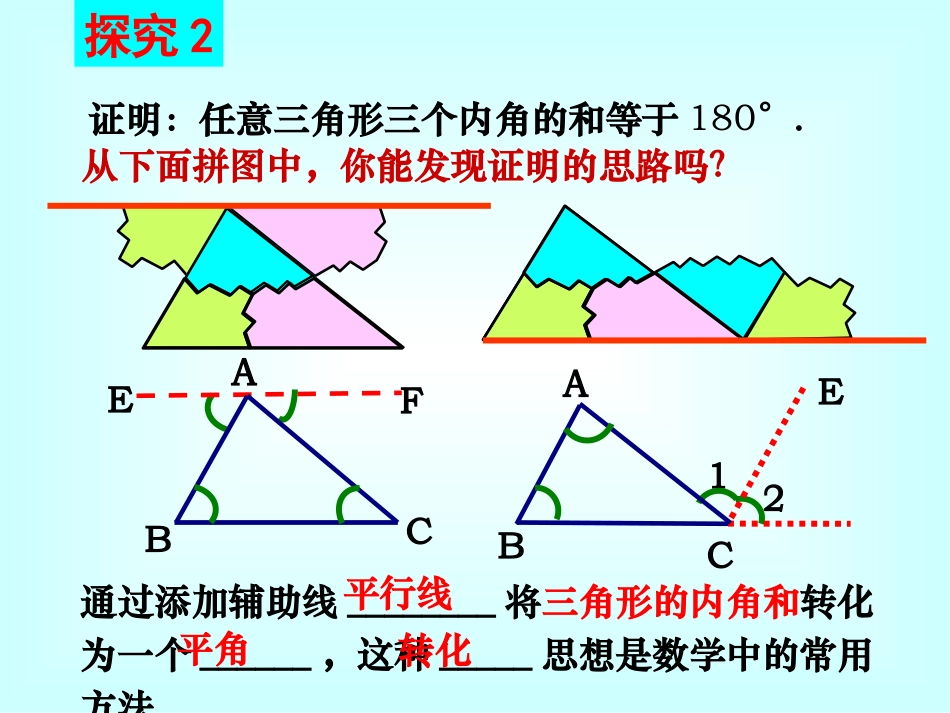
探究1ABC方法:折叠法.“三角形三个内角的和等于180°”探究2从下面拼图中,你能发现证明的思路吗?证明:任意三角形三个内角的和等于180°.FECBA21ECBA通过添加辅助线________将三角形的内角和转化为一个______,这种_____思想是数学中的常用方法.平行线平角转化过点A作直线EF∥BC∴∠2=B∠,∠3=C∠∵∠1+2+3=180∠∠°(平角定义)∴∠A+B+C=180∠∠°(等量代换)已知:△ABC.求证:∠A+B+C=180°∠∠∵EFBC∥1证明:例证1F23ECBA(两直线平行,内错角相等)21EDCBA延长BC到D,过C作CE∥BA,∴∠A=∠1(两直线平行,内错角相等)∠B=∠2(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°(等量代换)例证2证法二:已知:△ABC.求证:∠A+B+C=180°∠∠几种变形:∠A=180°–(B+C).∠∠∠B=_________________.∠C=_________________.三角形内角和定理:三角形三个内角的和等于180°.即在△ABC中,∠A+∠B+∠C=180°定理:∠A+B=180∠°-∠C.∠B+C=__________.∠∠A+C=__________.∠ABC例1、如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数.在△ABD中,∠ADB=180°-∠B-∠BAD,=180°-75°-20°=85°CABD75°40°解:∵AD是△ABC的角平分线,204021BAC21BAD例题:例2、如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?ADBCE北北∵ADBE∥∴∠DABABE∠=180°∴∠ABE=180°-∠DAB=180°-80°=100°在△ABC中,ACB∠=180°-∠CAB-∠ABC=180°-30°-60°=90°∴∠ABC=∠ABECBE∠=100°40°﹣=60°50°40°80°解:∠BAC=80°50°﹣=30°BDCE北A你还能想出求∠ACB的其他方法吗?1250°40°解:过点C作CFAD∥∴∠1=∠DAC=50°,F∵CFAD,∥又ADBE∥∴CFBE∥∴∠2=∠CBE=40°∴∠ACB=∠12﹢∠=50°40°﹢=90°1.如图,说出各图中∠1的度数.80°50°130°105°1(1)(2)课堂练习:2.△ABC中,若∠A+∠B=∠C,则△ABC是()A、锐角三角形B、直角三角形C、钝角三角形D、等腰三角形BDABC3、如图,从A处观测C处时仰角∠A=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?∠ACB=ACD∠-∠BCD=60°-45°=15°∠ACB=180°-(∠A+ABC∠)=180°-(30°+135°)=15°解:设三个内角度数分别为2x°、3x°、4x°,2x+3x+4x=180解得x=20∴三个内角度数分别为40°,60°,80°。80°60°40°4、在△ABC中,∠A:B:C=2:3:4∠∠,则∠A=____,B=∠C=∠.1.为什么要用推理的方法证明三角形的内角和定理?2.你是怎么找到三角形内角和定理的证明思路的?3.如何应用三角形内角和定理解决问题?课堂小结:1、课堂作业:教科书P16第1、3、7题.2、家庭作业:基础训练P8-P9基础夯实,P10核心导学.布置作业: