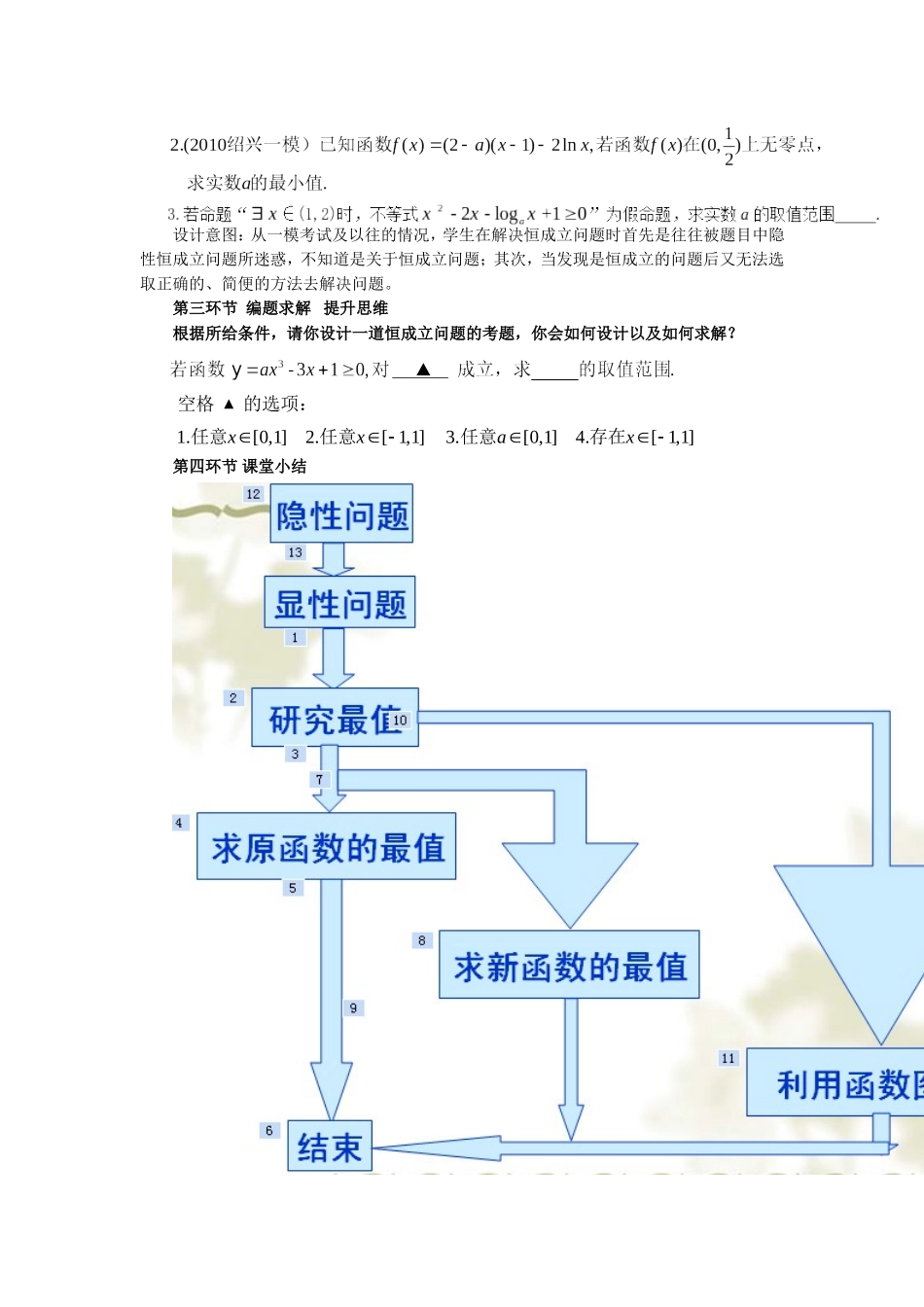
函数思想指导下的不等式恒成立问题的解决背景:一模结束后,对试题的分析,发现许多学生对22题的第2小题要么找不到解题方向,无法弄清题意;要么有方向但是不能善始善终,求得正确解。因此,我对不等式恒成立问题的解决设计了二个课时,对它进行一次专题复习,渗透函数思想,提高学生的处理能力,本堂课是此专题的第一课时。教学目标1.在问题的解决过程中,提炼归纳不等式恒成立的常见处理策略,把隐性不等式恒成立问题进行转化为显性恒成立问题,面对具体的问题学会选择解决方法。2.在自主探究和合作交流中,经历知识点产生和形成过程,不仅重视对研究的掌握和应用,更重视对研究方法的思想渗透以及分析问题和解决问题能力的培养,进一步提升理性思维能力,激发学生更积极主动的学习精神和和探究勇气。教学方法:探究式、启发式。教学重点与难点:不等式恒成立问题的解决方法选用。教学过程第一环节:回归课本提炼方法设计意图:越是高考最后的冲刺阶段越需要回过头来研读课本,而且近几年来浙江卷的试题还是以三次函数居多,所以引用了课本习题中的一题进行改编和变式,从简单的函数入手掌握解题方法,然后进行巩固、辨析、加深.范例:学生自行解题发现解决恒成立问题一般是两种解法.变式一:让学生在解题中自行体会两种解法的区别,便于以后能正确的选择.变式二:当前面两种方法都出现求解上的困难的时候,能否思考选用数形结合的思想,正确作出两个函数的图象,然后通过观察两图象(特别是交点时)的位置关系,列出关于参数的不等式。归纳总结第二环节化隐为显突出重围设计意图:从一模考试及以往的情况,学生在解决恒成立问题时首先是往往被题目中隐性恒成立问题所迷惑,不知道是关于恒成立问题;其次,当发现是恒成立的问题后又无法选取正确的、简便的方法去解决问题。第三环节编题求解提升思维根据所给条件,请你设计一道恒成立问题的考题,你会如何设计以及如何求解?第四环节课堂小结▲1.[0,1]2.[1,1]3.[0,1]4.[1,1]xxax空格的选项:任意任意任意存在▲检测练习1.函数在上单调递增,则实数m的取值范围为。2.若命题“”为假命题,则实数a的取值范围为。3.已知两函数,k为实数。(Ⅰ)对任意的,有成立,求实数k的取值范围;(Ⅱ)对任意的,,有成立,求实数k的取值范围;(Ⅲ)对任意的,总存在,有成立,求实数k的取值范围。4.设函数f(x)=(x+1)ln(x+1),若对所有的x0,都有f(x)ax成立,求实数a的取值范围.