转动动力学课件VIP免费

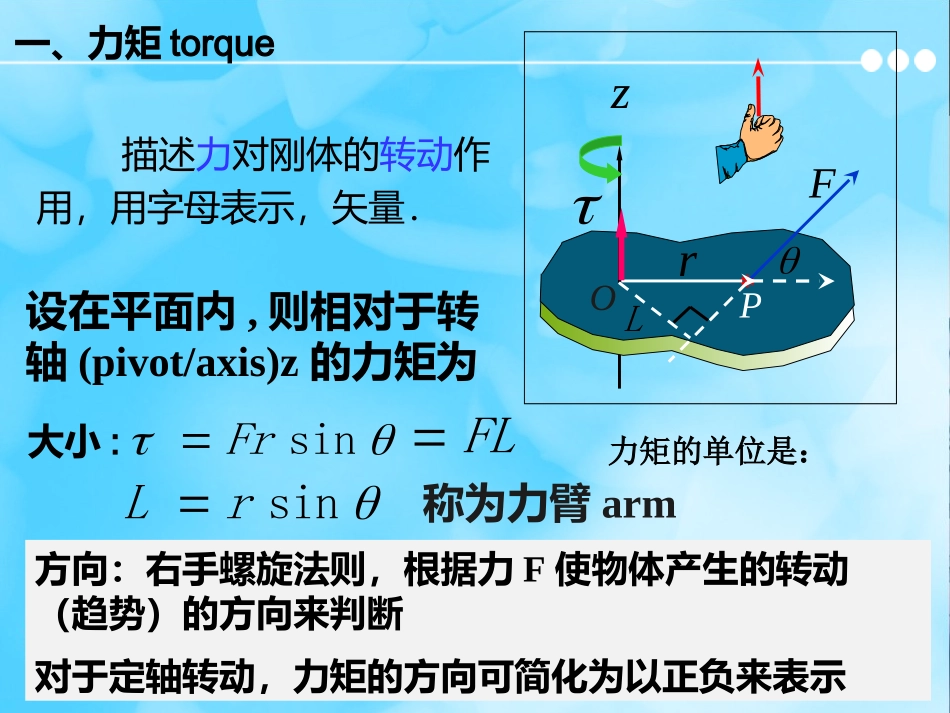
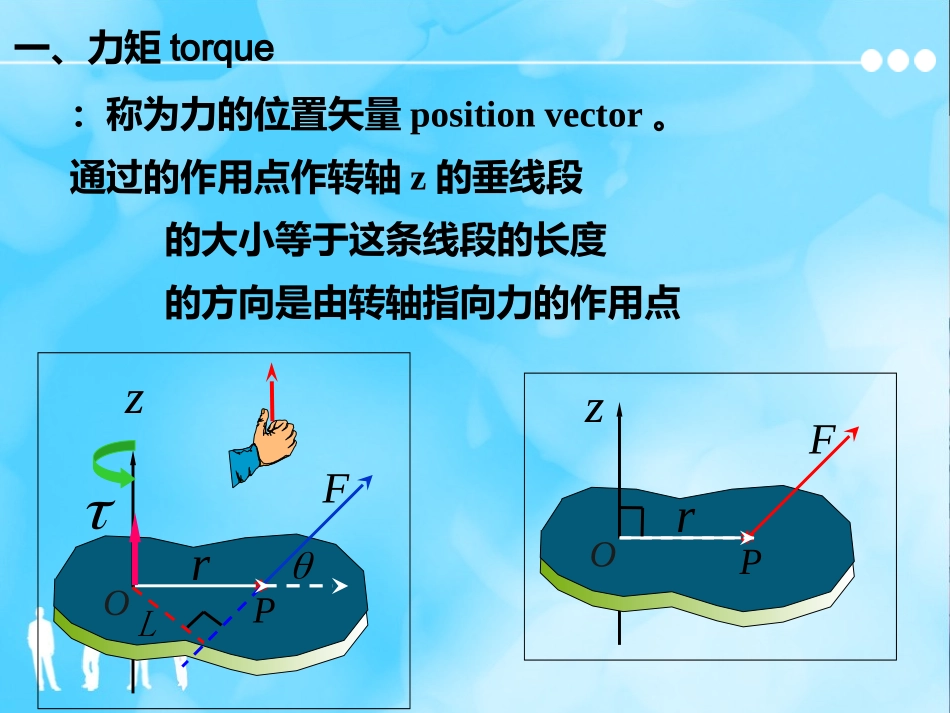
8.2转动动力学力矩转动惯量转动的牛顿第二定律一、力矩torque描述力对刚体的转动作用，用字母表示，矢量．Pz*OFrL设在平面内,则相对于转轴(pivot/axis)z的力矩为FL称为力臂armsinrL大小:sinFr方向：右手螺旋法则，根据力F使物体产生的转动（趋势）的方向来判断对于定轴转动，力矩的方向可简化为以正负来表示力矩的单位是：一、力矩torquePz*OFr：称为力的位置矢量positionvector。通过的作用点作转轴z的垂线段的大小等于这条线段的长度的方向是由转轴指向力的作用点Pz*OFrL二、净力矩（合力矩）nettorque1、合力矩等于各分力矩的矢量和2、合力为零，但合力矩不一定为零FFFF定轴转动直接求代数和，同向相加，反向相减𝝉𝒏𝒆𝒕=𝝉𝟏+𝝉𝟐+𝝉𝟑+⋯⋯𝝉𝒏𝒆𝒕=𝝉𝟏+𝝉𝟐+𝝉𝟑+⋯⋯合力：改变物体平动的运动状态合力矩：改变刚体转动的运动状态三、转动惯量rotationalinertia/momentofinertia转动惯量——描述物体转动惯性的大小的物理量。用字母表示，单位是定义：对于以Z为转轴的刚体上d的某一质点，若其与转轴之间的垂直距离为则该质点相对于转轴Z的转动惯量为Ozimir三、转动惯量rotationalinertia/momentofinertia对于以Z为转轴的刚体本身，由无数的质点(……、、、、)组成Ozimir则，这个刚体本身相对于转轴Z的转动惯量等于这所有质点相对于转轴Z的转动惯量之和。𝑰=𝑰𝟏+𝑰𝟐+𝑰𝟑+⋯+𝑰𝒏+⋯¿𝒎𝟏𝒓𝟏𝟐+𝒎𝟐𝒓𝟐𝟐+𝒎𝟑𝒓𝟑𝟐+⋯+𝒎𝒏𝒓𝒏𝟐+⋯三、转动惯量rotationalinertia/momentofinertia影响物体转动惯量大小的因素：1、物体的总质量总质量越大，转动惯量越大3、转轴的位置转轴位置不同，物体质量对轴的分布也就不同，导致转动惯量也不同。2、物体质量分布物体质量分布离转轴越远，转动惯量越大物体的质心离转轴的距离质量分布均匀特殊形状的几种物体的转动惯量三、转动惯量rotationalinertia/momentofinertia平行轴定理：三、转动惯量rotationalinertia/momentofinertia刚体质量为，设转轴通过其质心时转动惯量为若将此转轴朝任何方向平行移动一段距离则物体对于新转轴的转动惯量为推论：转轴通过质心时，物体的转动惯量最小CmAd四、刚体的定轴转动定律在质点运动中，力是引起质点运动状态变化的原因，力的作用使质点获得了加速度。这一物理过程的规律由牛顿第二定律来表示。Fma在刚体转动中，力矩是引起刚体转动状态变化的原因，力矩的作用使刚体获得了角加速度。这一物理过程的规律由刚体转动定律来描述。四、刚体的定轴转动定律刚体的定轴转动定律：刚体所受的对于某一固定转轴的合外力矩等于刚体对于此转轴的转动惯量与刚体在此合外力矩作用下所获得的角加速度的乘积。𝛼=𝜏净𝐼——转动的牛顿第二定律OZ适用条件：在转动过程中，刚体的转动惯量保持恒定不变。14比较IamFI是物体转动惯性的量度。m是物体平动惯性的量度。改变物体平动状态的原因aF改变物体转动状态的原因牛顿第二定律定轴转动定理I的意义：物体转动惯性的量度.由刚体的定轴转动定律可得出类似结论：相同作用下，较大的刚体，获得的小，刚体的转动状态很难改变，转动惯性大；较小的刚体，获得的大，转动状态容易改变，转动惯性小。总结：I表示刚体在转动过程中表现出来的惯性。一个外径和质量相同的实心圆柱与空心圆筒，若受力和力矩一样，谁转动得快些呢？MMI相对较大，a相对较小，转动较慢?质量分布影响演示实验𝛼=𝜏净𝐼茹科夫斯基凳图1图2