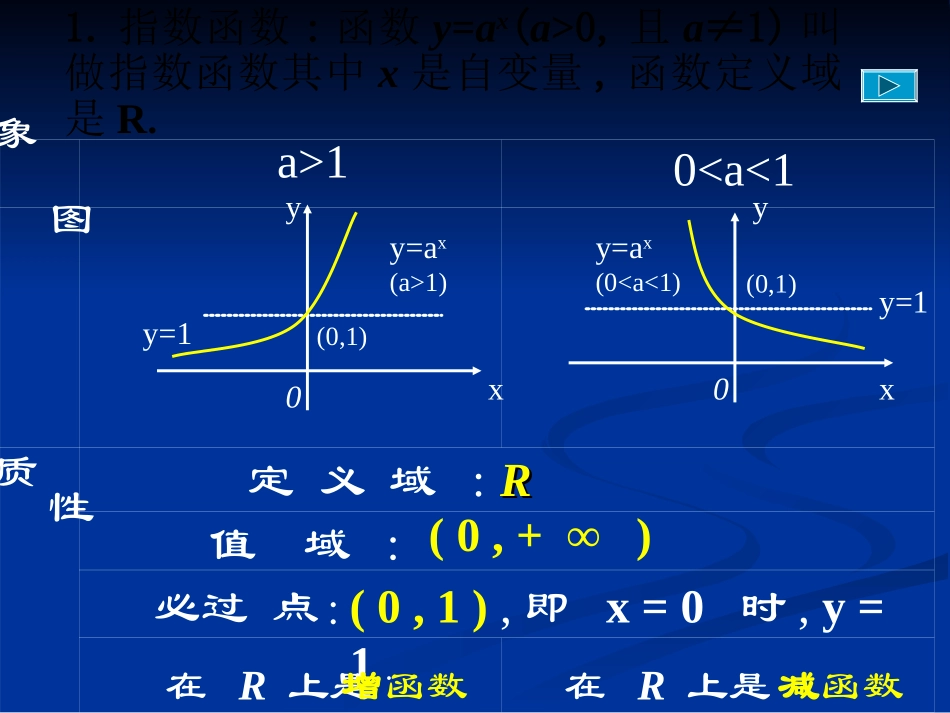
图象性质yx0y=1(0,1)y=ax(a>1)yx(0,1)y=10y=ax(0
100,且a≠1)叫做指数函数其中x是自变量,函数定义域是R.,已知131xay2.,)1,0(22aaayx?21yyx为何值时,练习复习引入复习引入3.函数y=ax-1+4恒过定点.A.(1,5)B.(1,4)C.(0,4)D.(4,0)练习例1:312122233xxyyx设,,确定为何指时,121212(1)(2)(3)yyyyyy有;;解、①、②、13125xxx由得,xR2y=是上的减函数,31215xyy时,;1215xyy时,;③、1215xyy时,;例2:指数函数模型截止1999年底,我国人口约13亿,如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国的人口数最多为多少(精确到亿)?小结:1、指数函数模型:A、指数增长型:设原有产值为N,平均增长率为P,则经过时间x后的总产值y可以用y=N(1+p)x表示.B、指数减少型:设原有产值为N,平均减少率为P,则经过时间x后的总产值y可以用y=N(1-p)x表示.C、指数型函数:把形如y=kax(k∈R,a>0且a≠1)的函数称为指数型函数。1.说明下列函数图象与指数函数y=2x的图象关系,并画出它们的图象:一、指数函数图象的变换;2,2(1)21xxyy;2,2(2)21xxyy.12,12)3(xxyyx-3-2-101230.1250.250.512480.250.51248160.51248163212xyxy222xy作出图象,显示出函数数据表212,2(1)xxyy987654321-4-224Oxy比较函数.的图象关系12xyxy222xy987654321-4-224Oxy比较函数.的图象关系12xyxy222xy987654321-4-224Oxy比较函数.的图象关系12xyxy222xyx-3-2-101230.1250.250.512480.06250.1250.250.51240.031250.06250.1250.250.51212xyxy222xy作出图象,显示出函数数据表212,2(2)xxyy987654321-4-224Oxy比较函数.的图象关系12xyxy222xy987654321-4-224Oxy比较函数.的图象关系12xyxy222xy987654321-4-224Oxy比较函数.的图象关系12xyxy222xy.12,12)3(xxyy987654321-4-224Oxy比较函数.的图象关系12xyxy212xy.12,12)3(xxyy987654321-4-224Oxy比较函数.的图象关系12xyxy212xy.12,12)3(xxyy987654321-4-224Oxy比较函数.的图象关系12xyxy212xy.12,12)3(xxyy小结:向左平移a个单位得到f(x+a)的图象;向右平移a个单位得到f(x-a)的图象;向上平移a个单位得到f(x)+a的图象;向下平移a个单位得到f(x)-a的图象.f(x)的图象例4.设a是实数,(1)试证明对于任意a,f(x)为增函数;2().21xfxa证明:任取x1,x2,且f(x1)-f(x2)=21222121xx12212222(21)(21)xxxx12212(22).(21)(21)xxxx∵y=2x在R上是增函数,且x1<x2,1222,xx12210,210,xx又12220.xx即∴f(x1)-f(x2)<0,即f(x1)<f(x2).故对于a取任意实数,f(x)为增函数.4.单调性与奇偶性问题12.xx解:若f(x)为奇函数,则f(-x)=-f(x),22(),2121xxaa即22221221xxxa22212xx.2利用f(0)=0例4.设a是实数,(2)试确定a的值,使f(x)为奇函数.2().21xfxa∴a=1.【1】已知定义域为R的函数为奇函数,则a=__,b=_____.1-2()2xxbfxa21(0)01;fb(1)(1)2.ffa【2】.求证函数是奇函数,且是增函数.21()21xxfx课堂小结1.指数复合函数的单调性和奇偶性;2.指数函数图象的变换.1.阅读教材P.54-P.58;2.《习案》作业十九.课后作业