6.1图上距离与实际距离-(3)VIP免费

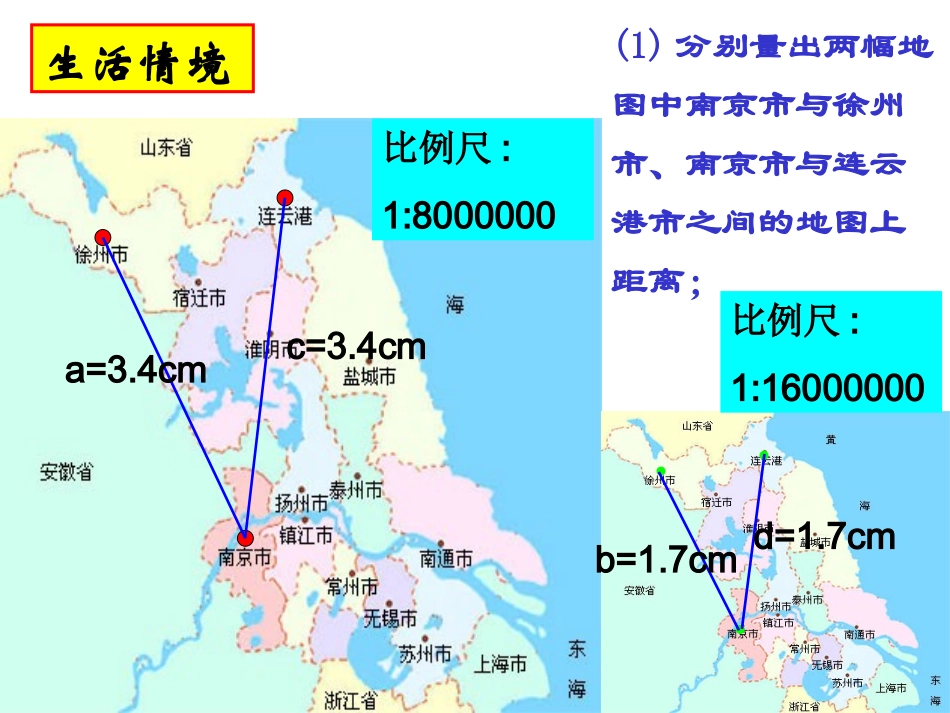
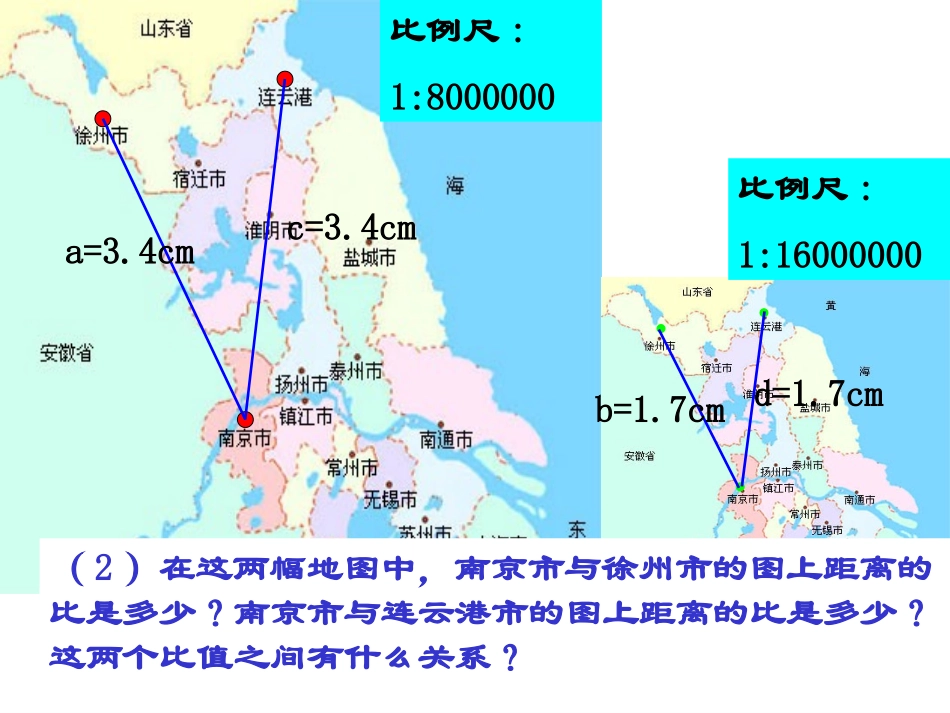
比例尺:1:8000000比例尺:1:16000000a=3.4cmd=1.7cmc=3.4cmb=1.7cm(1)分别量出两幅地图中南京市与徐州市、南京市与连云港市之间的地图上距离；生活情境比例尺:1:8000000比例尺:1:16000000a=3.4cmd=1.7cmc=3.4cmb=1.7cm（2）在这两幅地图中，南京市与徐州市的图上距离的比是多少？南京市与连云港市的图上距离的比是多少？这两个比值之间有什么关系？比例尺:1:8000000比例尺:1:16000000（３）在这两幅地图中，淮安与徐州的图上距离的比是多少？淮安与连云港的图上距离的比是多少？这两个比值之间又有怎样的关系呢？adcb两条线段长度的比叫线段的比四条线段a,b,c,d中，如果a与b的比等于c与d的比，即,那么这四条线段a,b,c,d叫做成比例线段，简称比例线段。::abcd新知总结例1：在比例尺为１：50000的地图上，测得A、B两地间的图上距离为16cm。求Ａ、Ｂ两地间的实际距离。图上距离比例尺实际距离典例探究淮安市的建设规划图上，城区南北长约为240㎝，而淮安市城区的南北实际长为18㎞，则规划图采用的比例尺是多少？小试身手例2：已知a、b、c、d是成比例线段，其中a＝３cm，b＝２cm，c＝６cm，求线段d的长．若条件改为a、b、d、c是成比例的4条线段，其它条件不变，线段d的长度是否改变？注意：成比例的四条线段，要注意其顺序性。典例探究比例的基本性质为：在比例中，两个外项的积等于两个内项的积.用式子表示就是：如果a:b=c:d或（b,d都不为0），那么ad=bc.反之，若ad=bc，则a:b=c:d或dc＝badc＝ba在中，若b=c,那么这时我们把b叫做a和d的比例中项.dc＝ba2bad变：已知a是b、c的比例中项，其中b＝２，c＝8，则a=_______．例3：已知a是线段b、c的比例中项，其中b＝２cm，c＝8cm，求线段a的长．典例探究例4已知＝，且x＋y＝24．求x、y的值．在小组中交流你的想法．x36.1图上距离与实际距离练习：（1）已知，求的值.23ba+23abab的值求且已知cbacbacba,,,68,141192例5：已知,求的值.21243yxyxyx151110accbba练习：已知,求a:b:c.abcdbd与dc＝ba如果，那么有什么样的关系呢？dcbaddcbba若有则有（１）abcdbd(2)ADEBC例5：如图，已知AD=15，AB=40，AC=28，且，求EC的长.ECAEDBAD典例探究ADEBC如图，求的值.23ADAEDBECABAEDBAC、及时巩固