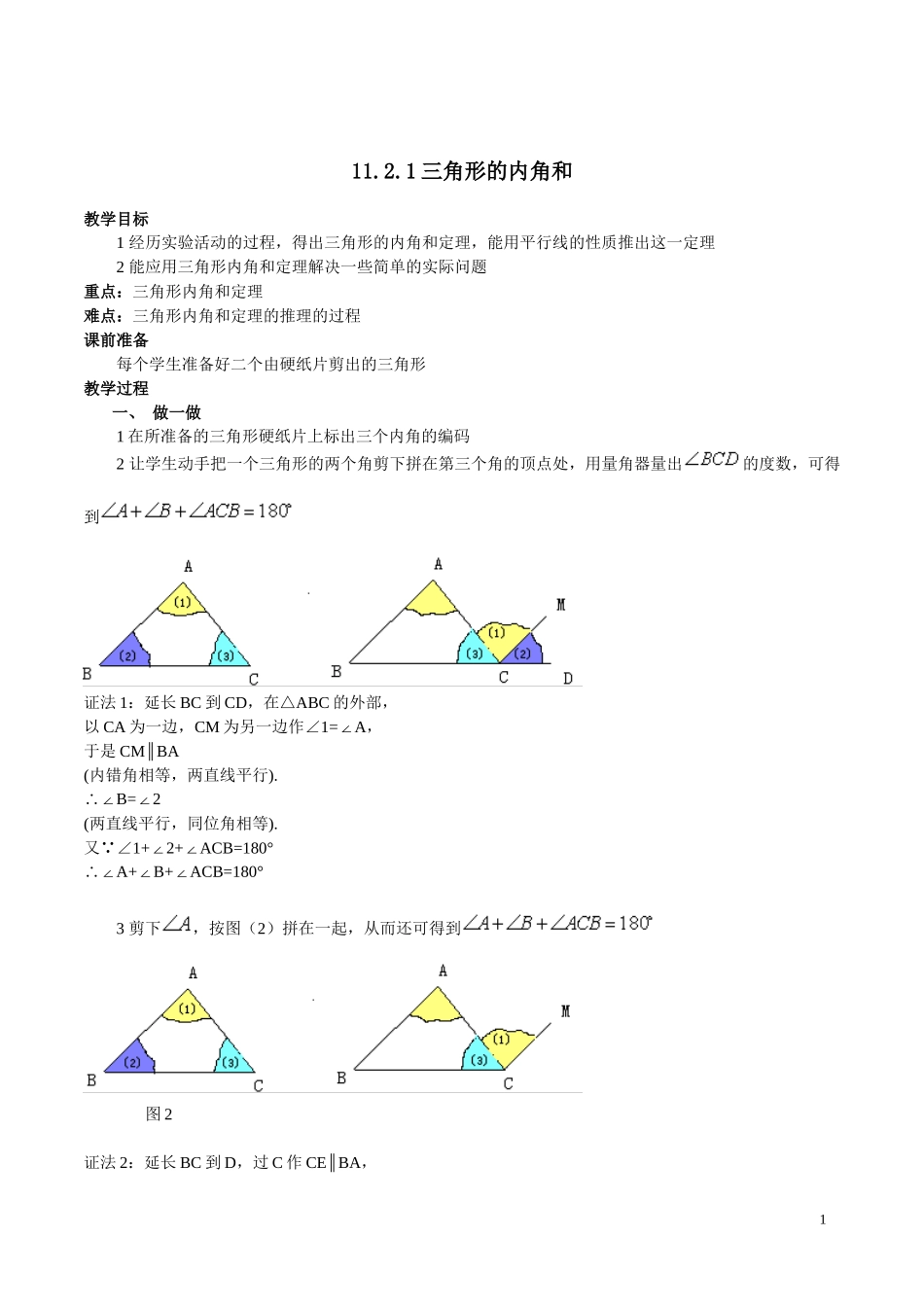
111.2.1三角形的内角和教学目标1经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理2能应用三角形内角和定理解决一些简单的实际问题重点:三角形内角和定理难点:三角形内角和定理的推理的过程课前准备每个学生准备好二个由硬纸片剪出的三角形教学过程一、做一做1在所准备的三角形硬纸片上标出三个内角的编码2让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到证法1:延长BC到CD,在△ABC的外部,以CA为一边,CM为另一边作∠1=A∠,于是CMBA∥(内错角相等,两直线平行).B=2∴∠∠(两直线平行,同位角相等).又∵∠1+2+ACB=180°∠∠A+B+ACB=180°∴∠∠∠3剪下,按图(2)拼在一起,从而还可得到图2证法2:延长BC到D,过C作CEBA∥,2A=1∴∠∠(两直线平行,内错角相等)B=2∠∠(两直线平行,同位角相等)又∵∠1+2+ACB=180°∠∠A+B+ACB=180°∴∠∠∠4把和剪下按图(3)拼在一起,用量角器量一量的度数,会得到什么结果。证法3:过A作MNBA∥,B=2∴∠∠(两直线平行,内错角相等)C=1∠∠(两直线平行,内错角相等)又∵∠2+1+BAC=180°∠∠B+C+BAC=180°∴∠∠∠新知运用:(1)在△ABC中,∠A=35°,∠B=43°则∠C=.(2)在△ABC中,∠A:∠B:∠C=2:3:4则∠A=∠B=∠C=.讨论:(1)一个三角形中最多有个直角?为什吗?(2)一个三角形中最多有个钝角?为什吗?(3)一个三角形中至少有个锐角?为什吗?(4)任意一个三角形中,最大的一个角的度数至少为.二、想一想3如果我们不用剪、拼的办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?已知,说明,你有几种方法?结合图(1)、图(2)、图(3)能不能用图(4)也可以说明这个结论成立三、例题如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?解:∠CAB=BAD-CAD=80°-50°=30°∠∠ADBE∵∥,得:∠BAD+BADE=180°∠ABE=180°-BAD=180°-80°=100°∴∠∠ABC=ABE-EBC=100°-40°=60°∠∠∠在△ABC中,∠ACB=180°-ABC-CAB∠∠=180°-60°-30°=90°答:从B岛看A,C两岛的视角∠ABC是60°,从C岛看A、B两岛的视角∠ACB是90°思考:2、在△ABC中,如果∠A=1/2B=∠1/3C∠,那么△ABC是什么三角形?四、练习:课本P13,练习1,2五、布置作业:4课本P16习题11.2.1第1,3,4,5题补充练习1三角形中最大的角是,那么这个三角形是锐角三角形()2一个三角形中最多只有一个钝角或直角()3一个等腰三角形一定是锐角三角形()4一个三角形最少有一个角不大于()