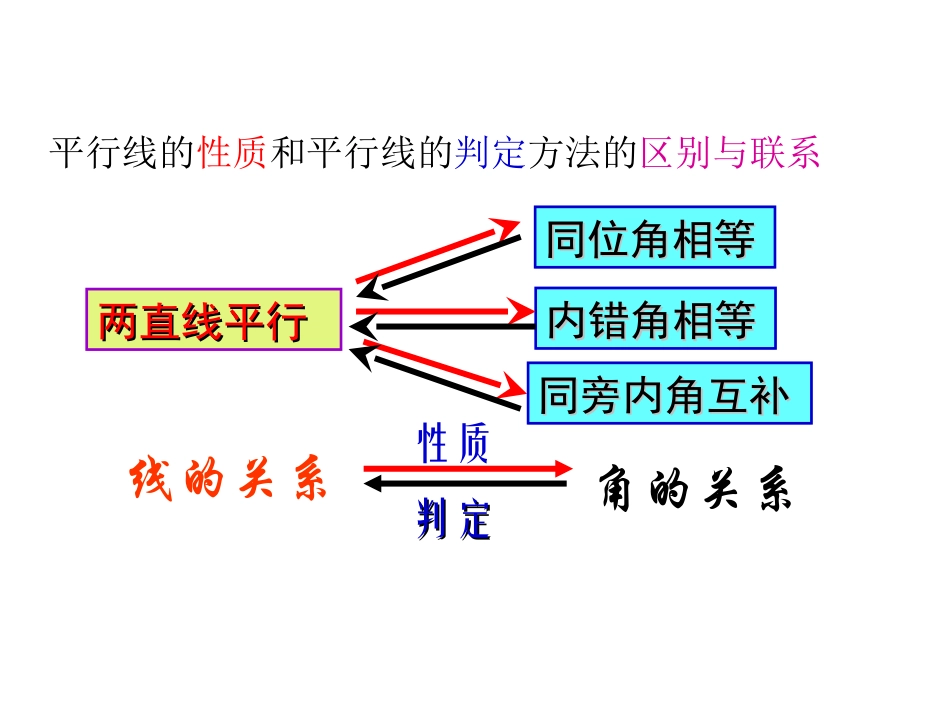
巧作平行线解决“拐点”问题铁城初级中学刘显清温故知新温故知新温故知新温故知新2、平行线的性质有哪些?1、平行线的判定方法有哪几种?3、它们之间有何区别与联系?两直线平行两直线平行同位角相等同位角相等内错角相等内错角相等同旁内角互补同旁内角互补线的关系角的关系判定判定性质平行线的性质和平行线的判定方法的区别与联系合作探究合作探究合作探究合作探究如图1,木杆AB与CD平行,BD是拉直的橡皮筋,在BD上任取一点E,试解答下列各题:(1)向左拉动点E,如图2所示,之间有何数量关系?DEB,,E图1ABECD图3AECDB图2DEB,,探究一:巧作一条平行线(2)向右拉动点E,如图3所示,之间有何数量关系?合作探究合作探究合作探究合作探究如图1,木杆AB与CD平行,BD是拉直的橡皮筋,在BD上任取一点E,现将图1中的橡皮筋拉成图2、图3的形状,试解答下列各题:(1)向左拉动点E,如图2所示,之间有何数量关系?DEB,,E图1AECDB图2探究一:巧作一条平行线合作探究合作探究合作探究合作探究如图1,木杆AB与CD平行,BD是拉直的橡皮筋,在BD上任取一点E,现将图1中的橡皮筋拉成图2、图3的形状,试解答下列各题:(2)向右拉动点A,如图3所示,之间有何数量关系?DEB,,E图1ABECD图3探究一:巧作一条平行线解:过点E作EF∥AB,∴∠B+∠BEF=180°(两直线平行,同旁内角互补)∵AB∥CD(已知)∴CD∥EF(平行于同一直线的两条直线互相平行)∴∠FED+∠D=180°(两直线平行,同旁内角互补)∴∠B+∠BEF+∠FED+∠D=360°即∠B+∠BED+∠D=360°巧作平行线解决“拐点”问题ABECD图3F合作探究合作探究合作探究合作探究探究一:巧作一条平行线合作探究合作探究合作探究合作探究如图1,木杆AB与CD平行,BD是拉直的橡皮筋,在BD上任取一点E,现将图1中的橡皮筋拉成图2、图3的形状,试解答下列各题:(3)你还能将图1中的橡皮筋拉成什么样的形状?你能画出相应的几何图形吗?并说明之间有何数量关系?探究一:巧作一条平行线E图1ABECD图3AECDB图2DEB,,ABECD图3AECDB图2ABCDE图4ABCDE图5ABCDE图7ABCDE图6∠E=B∠-∠D∠E=D∠-∠B∠E=D∠-∠B∠E=B∠-∠D∠E=B∠+D∠∠B+∠E+D∠=360°总结犀牛角型锄头型燕尾型铅笔型小结小结小结小结3、过“拐点”作平行线,把直线的关系问题转化为角度之间的关系问题。转化思想1、为解决平行线间的折线问题,可以过“拐点”作平行线,构造“三线八角”或“同时平行的三条直线”的基本图形。构造截线,使得平行线都有截线。2、作平行线的目的:1、一大门的栏杆(如图所示),BA垂直于地面AE于A,CD平行于地面AE,则=()180A、270B、280C、295D、2、如图,一条公路修到湖边时,需拐弯绕湖而过.如果第一次拐的∠A是120°,第二次拐的∠B是150°,如果第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度?为什么?BCDABCB∠C=150°练习合作探究合作探究合作探究合作探究从探究一的图2中,我们知道:当AB∥CD时,∠B,∠E,∠D之间存在一定的关系。试猜想:探究二:巧作多条平行线图(a)BAEFGDC(1)如图(a),AB∥DC,∠B,∠E,∠F,∠G,∠D之间又会有何关系?为什么?AECDB图2合作探究合作探究合作探究合作探究从探究一的图2中,我们知道:当AB∥CD时,∠B,∠E,∠D之间存在一定的关系。试猜想:探究二:巧作多条平行线(2)如图,AB∥CD,又能得到什么结论?小结小结小结小结有些简单的几何问题,如果抓住问题的实质,在实质不变的情况下,可以将问题进一步提升,得出一般性结论。练习A思考:(2)若将(1)中的条件与结论互换,是否依然成立?说明理由。(3)如图,若AB∥CD,试探究∠1+∠2+∠3+……+∠n的度数。∠1+∠2+∠3+∠4=540°练习练习2、课后思考题:布置作业布置作业布置作业布置作业1、《全效学习》20页;