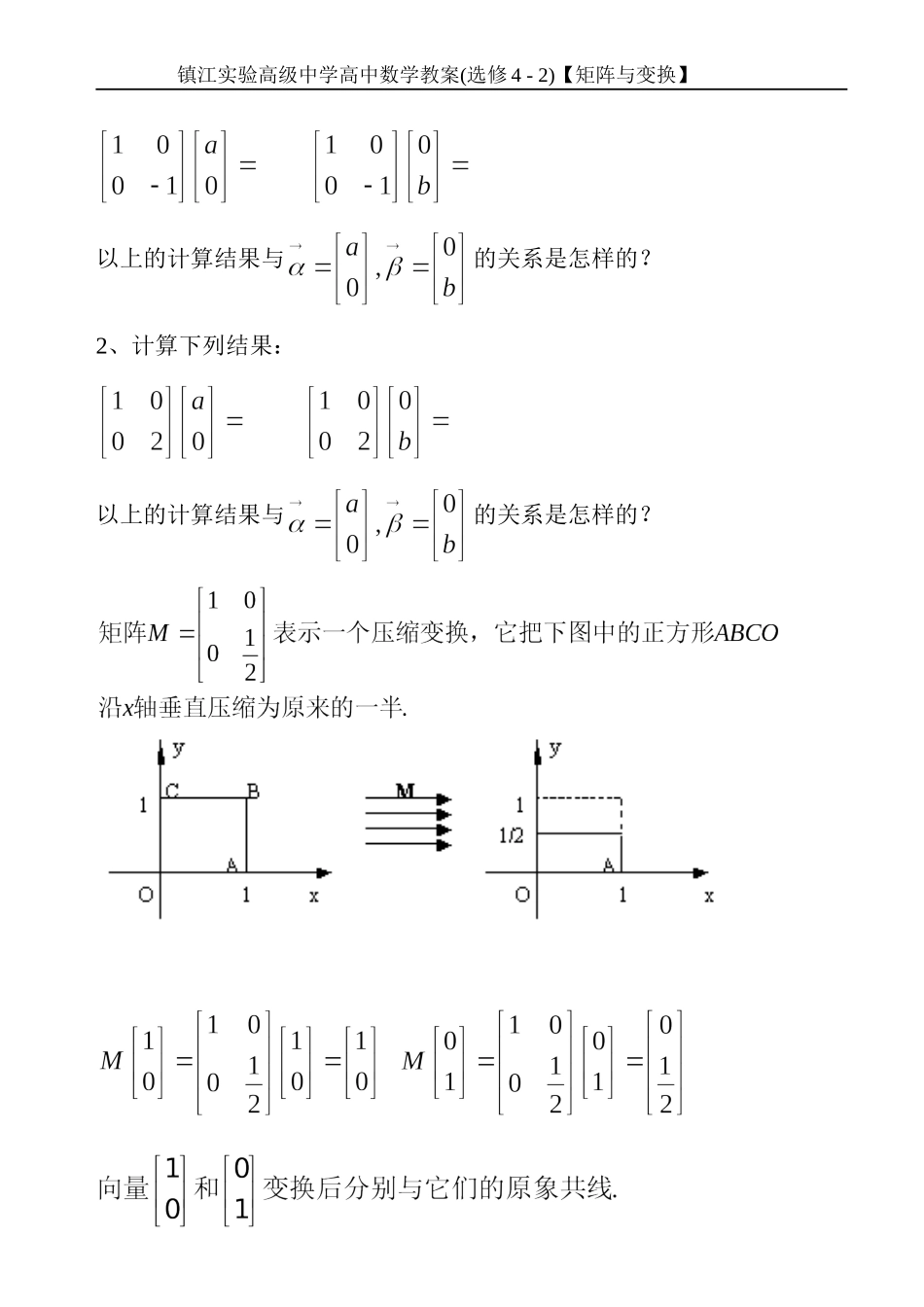
镇江实验高级中学高中数学教案(选修4-2)【矩阵与变换】§2.5.1特征值与特征向量1教学目标:1、知识与技能:1.掌握二阶矩阵特征值与特征向量的意义。2.会求二阶矩阵的特征值与特征向量(只要求特征值是两个不同实数的情形)。2、过程与方法:通过实例了解矩阵变换在向量共线中的作用,进而为引入特征值和特征向量的概念做好必要的铺垫.3、情感态度与价值观:以已有知识为平台,结合实例,创设良好情境,调动学生学习的积极性,发挥学生的主动性.重点难点:1、教学重点:会求二阶矩阵的特征值与特征向量。2、教学难点:二阶矩阵特征值与特征向量的意义。教学方法:自主合作探究教具准备:多媒体设备教学过程:问题探究、引入概念【情境】1、计算下列结果:镇江实验高级中学高中数学教案(选修4-2)【矩阵与变换】以上的计算结果与的关系是怎样的?2、计算下列结果:以上的计算结果与的关系是怎样的?镇江实验高级中学高中数学教案(选修4-2)【矩阵与变换】合作学习、形成概念设矩阵A=,如果对于实数,存在一个非零向量,使得A=,则称是矩阵A的一个特征值。是矩阵A的属于特征值的一个特征向量。从几何上看,特征向量的方向经过变换矩阵A的作用后,保持在同一条直线上。这时,特征向量或者方向不变(>0),或者方向相反(<0).特别地,当=0时,特征向量被变换成了0向量.设是矩阵A=的一个特征值,它的一个特征向量为,则,即满足方程组故,此时Dx=0、Dy=0因≠,所以xy不全为,则D=,即设矩阵A=,R,我们把行列式称为A的特征多项式。分析表明,如果是矩阵的特征值,则f,此时,将代入方程镇江实验高级中学高中数学教案(选修4-2)【矩阵与变换】组,得到一组非零解即为矩阵A的属于的一个特征向量【引例】求出矩阵A=的特征值和特征向量。总结求二阶矩阵特征值与特征向量的步骤,并思考能否从几何变换的角度直接观察出矩阵A的特征向量?【定理1】如果是矩阵A的属于特征值的一个特征向量,则对任意的非零常数t,t也是矩阵A的属于特征值的特征向量。其几何意义是:属于矩阵的同一个特征值的特征向量共线.【思考】属于矩阵的不同特征值的特征向量有何关系?【定理2】属于矩阵的不同特征值的特征向量不共线。学以致用、深化概念【例1】【评析】:【例2】【评析】:【例3】镇江实验高级中学高中数学教案(选修4-2)【矩阵与变换】【评析】:自主探究、巩固概念总结反思、提高认识课外作业:教学反馈: