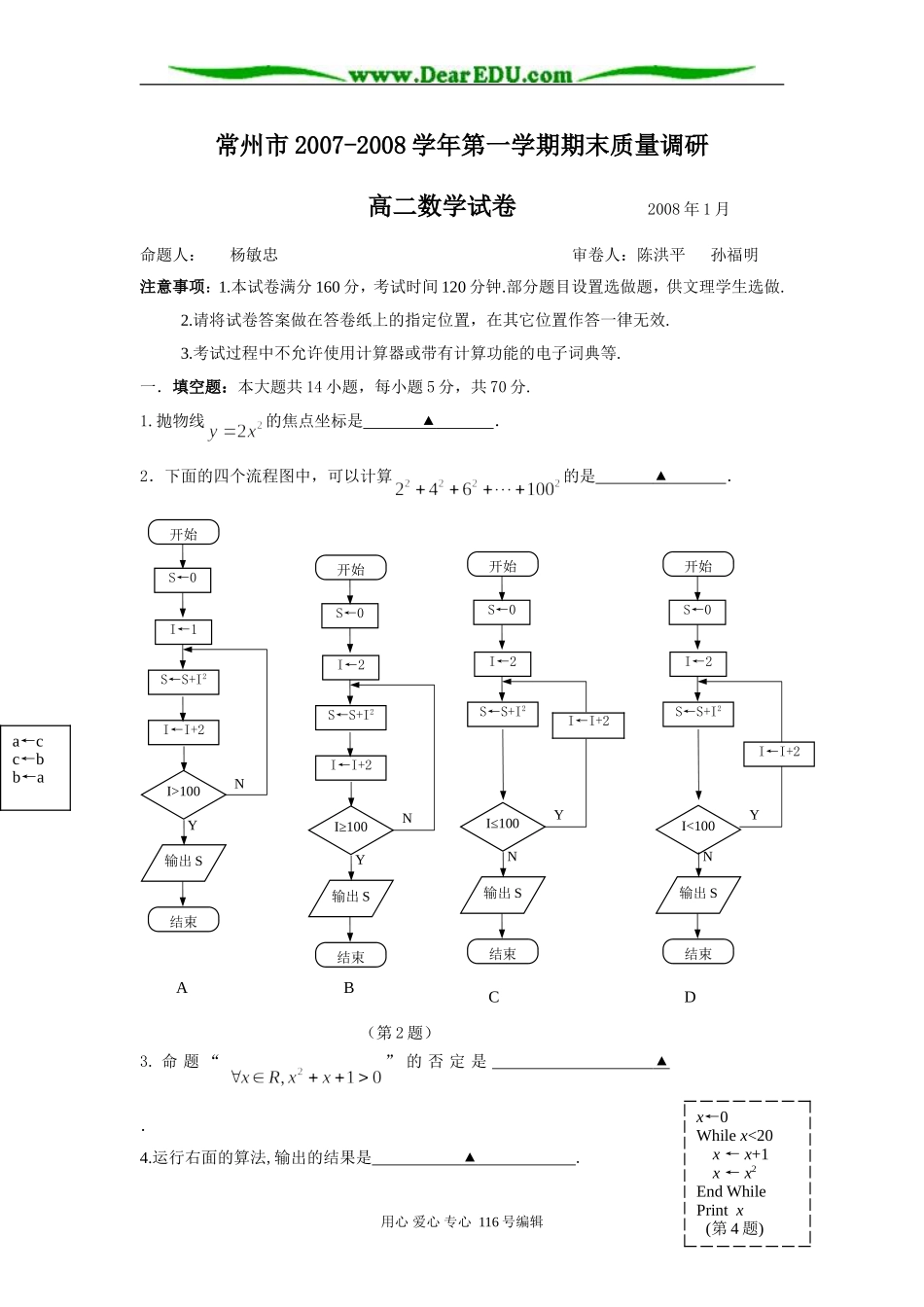
开始I←2S←S+I2S←0I←I+2I≥100输出S结束NY开始I←2S←S+I2S←0I≤100输出S结束CYNI←I+2开始I←2S←S+I2S←0I<100输出S结束DYNI←I+2Bx←0Whilex<20x←x+1x←x2EndWhilePrintx(第4题)常州市2007-2008学年第一学期期末质量调研高二数学试卷2008年1月命题人:杨敏忠审卷人:陈洪平孙福明注意事项:1.本试卷满分160分,考试时间120分钟.部分题目设置选做题,供文理学生选做.2.请将试卷答案做在答卷纸上的指定位置,在其它位置作答一律无效.3.考试过程中不允许使用计算器或带有计算功能的电子词典等.一.填空题:本大题共14小题,每小题5分,共70分.1.抛物线的焦点坐标是▲.2.下面的四个流程图中,可以计算的是▲.(第2题)3.命题“”的否定是▲.4.运行右面的算法,输出的结果是▲.用心爱心专心116号编辑开始I←1S←S+I2S←0I←I+2I>100输出S结束NYa←cc←bb←aA5.若施肥量千克与水稻产量千克的线性回归方程为则当施肥量为80千克时,预计水稻产量为▲千克.6.甲、乙两个总体各抽取一个样本,若甲样本均值为15,乙样本均值为17,甲样本方差为3,乙样本方差为2,则总体▲(填写“甲”或“乙”)波动小.7.(文)如果质点的位移与时间满足方程(位移单位:米,时间单位:秒),则质点在时的瞬时速度为▲米/秒.(理)已知△的三个顶点为(3,3,2),(4,-3,7),(0,5,1),为边的中点,则▲.8.容量为100的样本的频率分布直方图如图所示,则样本数据落在范围内的频率为▲.9.(文)已知函数,则=▲.(理)已知向量a=(2,-1,3),b=(-1,4,-2),c=(7,0,λ),若a、b、c三个向量共面,则实数λ=▲.10.已知一纸箱内装有某种矿泉水12瓶,其中有2瓶不合格,若质检人员从该纸箱内随机抽出2瓶,则检测到不合格产品的事件概率是▲.11.中心在原点,长轴长为8,准线方程为的椭圆标准方程为▲.12.在面积为2的正三角形内任取一点,则使的面积小于1的概率为▲.13.(文)若函数在上单调递减,则实数的取值范围是▲.(理)设为坐标原点,向量,,,点在直线上运动,则当取得最小值时,点的坐标为▲.14.有如下四个命题:命题①:方程表示焦点在轴上的椭圆;命题②:是直线和直线互相垂直的充要条件;命题③:方程表示离心率大于的双曲线;用心爱心专心116号编辑(第8题)命题④:“全等三角形的面积相等”的否命题.其中真命题的序号是▲.(写出所有真命题的序号)二.解答题:本大题共6小题,每小题15分,共90分.解答应写出文字说明、证明过程或演算步骤.15.(I)若抛物线的焦点是椭圆左顶点,求此抛物线的标准方程;(II)若双曲线与椭圆有相同的焦点,与双曲线有相同渐近线,求此双曲线的标准方程.16.先后抛掷一枚形状为正方体的骰子(正方体的六个面上分别标以数字),骰子向上的点数依次为.(I)共有多少个基本事件?(II)设“”为事件,求事件发生的概率;(Ⅲ)设“”为事件,求事件发生的概率.17.已知:方程表示椭圆;:抛物线与轴无公共点,若是真命题且是假命题,求实数的取值范围.18.(文)某种新型快艇在某海域匀速行驶中每小时的耗油量(升)关于行驶速度(千米/小时)的函数解析式可以表示为:该海域甲、乙两地相距120千米.(I)当快艇以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?(II)当快艇以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少约为多少升?(精确到0.1升).(理)已知空间三点(0,2,3),(-2,1,6),(1,-1,5).(I)若向量a=()分别与向量垂直,求向量a的坐标.(II)求以向量为一组邻边的平行四边形的面积的值.19.(文)双曲线的中心是原点O,它的一个焦点为,离心率e=.(I)求双曲线的方程;(II)求过点(2,1)且与曲线有且仅有一个公共点的直线方程.用心爱心专心116号编辑A1AB1BC1CD1DxyzFE(理)已知平面内动点(,)到定点与定直线:的距离之比是常数.(I)求动点的轨迹及其方程;(II)求过点(2,1)且与曲线有且仅有一个公共点的直线方程.20.(文)已知函数与直线切于点(,1).(Ⅰ)求实数的值;(Ⅱ)若时,不等式恒成立,求实数的取值范围.(理)已知正四棱柱底面边长,侧棱的长为4,过点作的垂线交侧棱于点,交线段于点.以为原点,、、所在直线分别为、、轴建立空间直角坐标系,如图.(Ⅰ)求证:平面;(Ⅱ)求与平面所成角的正弦值的大小.用心爱心专心116号编辑