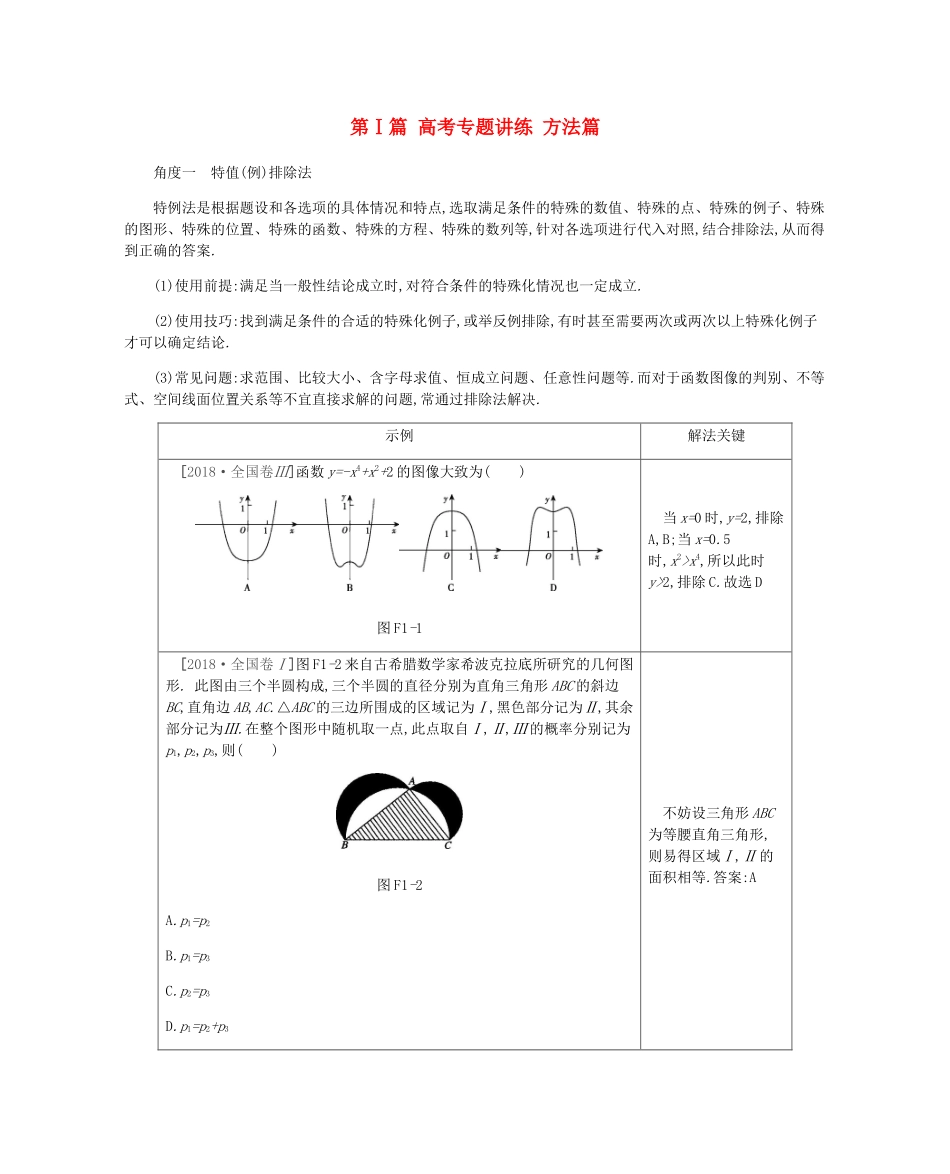
第Ⅰ篇高考专题讲练方法篇角度一特值(例)排除法特例法是根据题设和各选项的具体情况和特点,选取满足条件的特殊的数值、特殊的点、特殊的例子、特殊的图形、特殊的位置、特殊的函数、特殊的方程、特殊的数列等,针对各选项进行代入对照,结合排除法,从而得到正确的答案.(1)使用前提:满足当一般性结论成立时,对符合条件的特殊化情况也一定成立.(2)使用技巧:找到满足条件的合适的特殊化例子,或举反例排除,有时甚至需要两次或两次以上特殊化例子才可以确定结论.(3)常见问题:求范围、比较大小、含字母求值、恒成立问题、任意性问题等.而对于函数图像的判别、不等式、空间线面位置关系等不宜直接求解的问题,常通过排除法解决.示例解法关键[2018·全国卷Ⅲ]函数y=-x4+x2+2的图像大致为()图F1-1当x=0时,y=2,排除A,B;当x=0.5时,x2>x4,所以此时y>2,排除C.故选D[2018·全国卷Ⅰ]图F1-2来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则()图F1-2A.p1=p2B.p1=p3C.p2=p3D.p1=p2+p3不妨设三角形ABC为等腰直角三角形,则易得区域Ⅰ,Ⅱ的面积相等.答案:A[2016·全国卷Ⅱ]函数y=Asin(ωx+φ)的部分图像如图F1-3所示,则()图F1-3A.y=2sin2x-π6B.y=2sin2x-π3C.y=2sinx+π6D.y=2sinx+π3令x=0和x=π3,验证可得结果.答案:A[2017·全国卷Ⅰ]已知α∈(0,π2),tanα=2,则cos(α−π4)=.取角α终边上特殊点(1,2),利用定义代入计算,求sinα,cosα.答案:3❑√1010[2017·全国卷Ⅰ]函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是()A.[-2,2]B.[-1,1]C.[0,4]D.[1,3]当x=4时,f(x-2)=f(2)
b>0,且ab=1,则下列不等式成立的是()A.a+1bb|b|,则下列不等式一定成立的是()A.a3>b3B.a2>b2C.1a<1bD.log12|a|0,0,x=0,-1,x<0,则函数f(x)=sinx·sgnx的图像大致是()ABCD图F1-43.已知函数f(x)={-x2+ax,x≤1,a2x-7a+14,x>1,若存在x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),则实数a的取值范围为()A.a<2B.34,x-ay≤2},则()A.对任意实数a,(2,1)∈AB.对任意实数a,(2,1)∉AC.当且仅当a<0时,(2,1)∉AD.当且仅当a≤32时,(2,1)∉A对a取数字验证.a=0时,A错;a=2时,B错;a=32时,C错.所以选D[2018·全国卷Ⅰ]已知函数f(x)=2cos2x-sin2x+2,则()A.f(x)的最小正周期为π,最大值为3B.f(x)的最小正周期为π,最大值为4C.f(x)的最小正周期为2π,最大值为3D.f(x)的最小正周期为2π,最大值为4当sinx=0,cosx=1时,函数值为4,所以A,C错;把x+π代入验证,可得f(x+π)=f(x),说明D错.故选B[2018·全国卷Ⅲ]下列函数中,其图像与函数y=lnx的图像关于直线x=1对称的是()A.y=ln(1-x)B.y=ln(2-x)C.y=ln(1+x)D.y=ln(2+x)函数y=lnx的图像过定点(1,0),而(1,0)关于直线x=1对称的点还是(1,0),将(1,0)代入选项验证.答案...