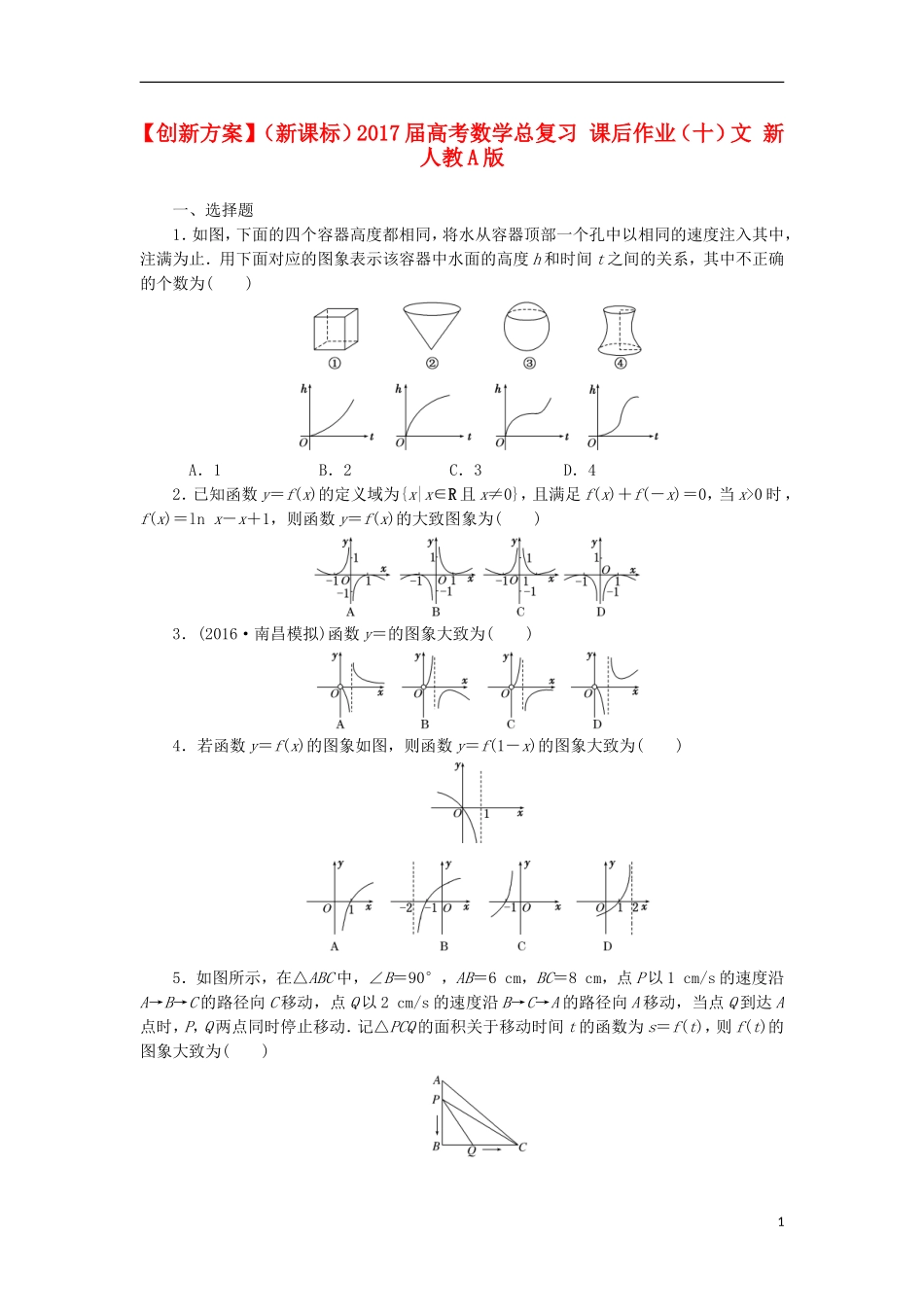
【创新方案】(新课标)2017届高考数学总复习课后作业(十)文新人教A版一、选择题1.如图,下面的四个容器高度都相同,将水从容器顶部一个孔中以相同的速度注入其中,注满为止.用下面对应的图象表示该容器中水面的高度h和时间t之间的关系,其中不正确的个数为()A.1B.2C.3D.42.已知函数y=f(x)的定义域为{x|x∈R且x≠0},且满足f(x)+f(-x)=0,当x>0时,f(x)=lnx-x+1,则函数y=f(x)的大致图象为()3.(2016·南昌模拟)函数y=的图象大致为()4.若函数y=f(x)的图象如图,则函数y=f(1-x)的图象大致为()5.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P以1cm/s的速度沿A→B→C的路径向C移动,点Q以2cm/s的速度沿B→C→A的路径向A移动,当点Q到达A点时,P,Q两点同时停止移动.记△PCQ的面积关于移动时间t的函数为s=f(t),则f(t)的图象大致为()1二、填空题6.函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)=________.7.直线y=1与曲线y=x2-|x|+a有四个交点,则a的取值范围是________.8.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为________.三、解答题9.已知函数f(x)=x|m-x|(x∈R),且f(4)=0.(1)求实数m的值;(2)作出函数f(x)的图象;(3)根据图象指出f(x)的单调递减区间;(4)若方程f(x)=a只有一个实数根,求a的取值范围.10.设函数f(x)=x+的图象为C1,C1关于点A(2,1)的对称图形为C2,C2对应的函数为g(x).(1)求函数g(x)的解析式;(2)若直线y=b与C2有且仅有一个公共点,求b的值,并求出交点的坐标.1.(2015·新课标全国卷Ⅰ)设函数y=f(x)的图象与y=2x+a的图象关于直线y=-x对称,且f(-2)+f(-4)=1,则a=()A.-1B.1C.2D.42.(2016·邵阳模拟)已知正方形OABC的四个顶点O(0,0),A(1,0),B(1,1),C(0,1),设u=2xy,v=x2-y2,是一个由平面xOy到平面uOv上的变换,则正方形OABC在这个变换下的图形是()3.已知函数f(x)=则函数y=f(1-x)的大致图象是()4.已知函数f(x)=其中[x]表示不超过x的最大整数.若直线y=k(x+1)(k>0)与函数y=f(x)的图象恰有三个不同的交点,则实数k的取值范围是________.5.当x∈(1,2)时,不等式(x-1)20时,f(x)=lnx-x+1,则f′(x)=-1=,x>0,所以x∈(0,1)时,f′(x)>0,f(x)单调递增,排除B,故选A.3.解析:选D当00,lnx<0,∴y<0,图象在x轴下方;当x>1时,2x>0,lnx>0,∴y>0,图象在x轴上方,当x→+∞时,y=是递增函数.4.解析:选A由函数y=f(x)的图象可得函数定义域是(-∞,1),所以1-x<1,解得x>0,即函数y=f(1-x)的定义域为(0,+∞).5.解析:选A当0≤t≤4时,点P在AB上,点Q在BC上,此时PB=6-t,CQ=8-2t,则s=f(t)=QC×BP=(8-2t)×(6-t)=t2-10t+24;当4≤t≤6时,点P在AB上,点Q在CA上,此时AP=t,P到AC的距离为t,CQ=2t-8,则s=f(t)=QC×t=(2t-8)×t=(t2-4t);当6≤t≤9时,点P在BC上,点Q在CA上,此时CP=14-t,QC=2t-8,则s=f(t)=QC×CPsin∠ACB=(2t-8)·(14-t)×=(t-4)·(14-t).综上,函数f(t)对应的图象是三段抛物线,依据开口方向得图象是A.二、填空题6.解析:与曲线y=ex关于y轴对称的曲线为y=e-x,函数y=e-x的图象向左平移1个单位长度即可得到函数f(x)的图象,即f(x)=e-(x+1)=e-x-1.答案:e-x-17.解析:y=作出图象,如图所示....